
【题目】小王从同事小李手中接收一批生产任务,派单方要求必须在15天内完成,届时承以每件60元的价格全部回收,小王在接受任务之后,其生产的任务y(件)与生产的天数x(天)关系如图1所示,其中在生产6天之后,每天的生产数量达到了30件.
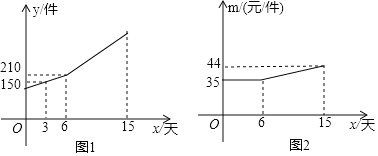
(1)求y与x之间的函数表达式;
(2)设第x天生产的产品成本为m元/件,m与x的函数图象如图2所示,若小王第x天的利润为W元,求W与x的关系式,并求出第几天后小王的利润可达到最大值,最大值为多少?
【答案】(1)![]() ;(2)当1≤x≤6时,W1=500x+2250(1≤x≤6);当6<x≤15时,W2=﹣30(x﹣15)2+7680(6<x≤15);第15天后小王的利润可达到最大值,最大值为7680.
;(2)当1≤x≤6时,W1=500x+2250(1≤x≤6);当6<x≤15时,W2=﹣30(x﹣15)2+7680(6<x≤15);第15天后小王的利润可达到最大值,最大值为7680.
【解析】
(1)分当1≤x≤6、6<x≤15时,分别求解即可;
(2)分1≤x≤6、6<x≤15,分别求解即可.
解:(1)①当1≤x≤6时,设函数的表达式为:y=kx+b,
由题意得:![]() ,解得:
,解得:![]() ,
,
y1=20x+90(1≤x≤6);
②当6<x≤15时,同理可得:y2=30x+30(6<x≤15);
故函数的表达式为:y=![]() ;
;
(2)①当1≤x≤6时,m1=35,
②当6<x≤15时,同理可得:m2=x+29(6<x≤15),
故m=![]() ;
;
故当1≤x≤6时,
每件产品的利润为60﹣35=25,
总利润W1=25(20x+90)=500x+2250(1≤x≤6);
当6<x≤15时,
每件产品的利润为60﹣(x+29)=﹣x+31,
W2=(30x+30)(﹣x+31)=﹣30(x﹣15)2+7680(6<x≤15),
故当x=15时,函数有最大值7680,
故:第15天后小王的利润可达到最大值,最大值为7680.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点,则下列结论:①△ADF≌△FEC;②四边形ADEF为菱形;③![]() 。其中正确的结论是____________.(填写所有正确结论的序号)
。其中正确的结论是____________.(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象经过第一象限内的一点A(n,4),过点A作AB⊥x轴于点B,且△AOB的面积为2.
的图象经过第一象限内的一点A(n,4),过点A作AB⊥x轴于点B,且△AOB的面积为2.
(1)求m和n的值;
(2)若一次函数y=kx+2的图象经过点A,并且与x轴相交于点C,求线段AC的长.
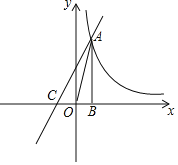
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
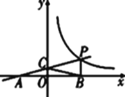
(1)求一次函数、反比例函数的解析式;
(2)求证:点C为线段AP的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,等边△ABC中D点为AB边上一动点,E为直线AC上一点,将△ADE沿着DE折叠,点A落在直线BC上,对应点为F,若AB=4,BF:FC=1:3,则线段AE的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+6与x轴、y轴分别交于A、B两点,点P是以C(﹣1,0)为圆心,1为半径的圆上一点,连接PA,PB,则△PAB面积的最大值为_____.
x+6与x轴、y轴分别交于A、B两点,点P是以C(﹣1,0)为圆心,1为半径的圆上一点,连接PA,PB,则△PAB面积的最大值为_____.
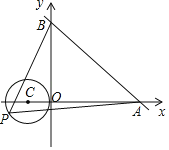
查看答案和解析>>
科目:初中数学 来源: 题型:
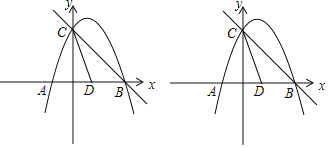
【题目】如图,抛物线y=﹣x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(﹣1,0),C(0,3)
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在P点,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
(3)在BC上方的抛物线上,是否存在点E,使得△BCE的面积最大?若存在,求出点E的坐标和△BCE的面积最大值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
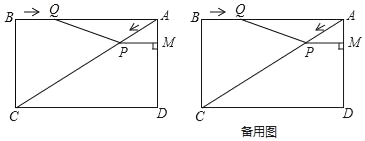
【题目】已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
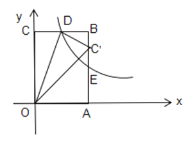
【题目】如图,平面直角坐标系中,矩形ABCD与双曲线![]() 交于D、E两点,将△OCD沿OD翻折,点C的对称C'恰好落在边AB上,已知OA=3,OC=5,则AE长为()
交于D、E两点,将△OCD沿OD翻折,点C的对称C'恰好落在边AB上,已知OA=3,OC=5,则AE长为()
A. 4B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com