
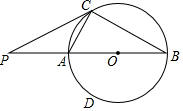
 在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.
在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.分析 (1)连接OC,由切线的性质得出OC⊥PC,推出∠PCA+∠ACO=90°,由圆周角定理得出∠B+∠CAB=90°,证出∠OAC=∠OCA,推出∠B+∠OCA=90°,得出∠PCA=∠B,即可得出结论;
(2)①当点Q运动到OQ⊥AB时,四边形AQBC的面积最大;连接AQ、BQ,由线段垂直平分线性质得出OQ=BQ,由圆周角定理得出∠AQB=90°,证出△ABQ是等腰直角三角形,得出AQ=$\frac{\sqrt{2}}{2}$AB=3$\sqrt{2}$,
②由直角三角形的性质和圆周角定理得出AC=$\frac{1}{2}$AB=3,BC=$\sqrt{3}$AC=3$\sqrt{3}$,分两种情况讨论,由全等三角形的判定即可得出结论.
解答 (1)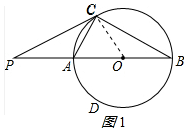 证明:如图1所示,连接OC.
证明:如图1所示,连接OC.
∵PC是圆O的切线,OC是半径,
∴OC⊥PC,
∴∠PCO=90°
∴∠PCA+∠ACO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠B+∠CAB=90°,
∵OC=OA,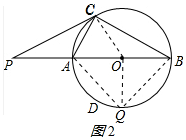
∴∠OAC=∠OCA,
∴∠B+∠OCA=90°,
∴∠PCA=∠B,
又∵∠P=∠P,
∴△PAC∽△PCB;
(2)解:①当点Q运动到OQ⊥AB时,四边形AQBC的面积最大;
如图2所示:连接AQ、BQ,
∵OA=OB,OQ⊥AB,
∴OQ=BQ,
∵AB是直径,
∴∠AQB=90°,
∴△ABQ是等腰直角三角形,
∴AQ=$\frac{\sqrt{2}}{2}$AB=3$\sqrt{2}$,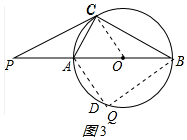
故答案为:3$\sqrt{2}$;
②如图3所示:∵∠ACB=90°,∠ABC=30°,
∴AC=$\frac{1}{2}$AB=3,BC=$\sqrt{3}$AC=3$\sqrt{3}$,
分两种情况:
a.当AQ=AC=3时,
在Rt△ABC和Rt△ABQ中,$\left\{\begin{array}{l}{AB=AB}\\{AC=AQ}\end{array}\right.$,
∴△ABC≌△ABQ(HL);
b.当AQ=BC=3$\sqrt{3}$时,同理△ABC≌△BAQ;
综上所述:当AQ=3或3$\sqrt{3}$时,△ABC与△ABQ全等.
点评 本题是圆的综合题目,考查了圆周角定理、相似三角形的判定与性质、切线的性质、线段垂直平分线的性质、等腰直角三角形的判定与性质、勾股定理、等腰三角形的性质、全等三角形的判定与性质等知识;本题综合性强,有一定难度.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
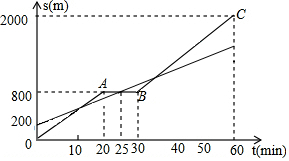 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
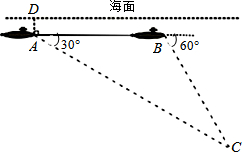 如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )| A. | 2000米 | B. | 4000米 | C. | 2000$\sqrt{3}$米 | D. | (2000$\sqrt{3}$+500)米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com