
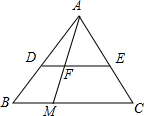
 如图,已知△ABC,DE∥BC,交AB于点D,交AC于点E,点M在边BC上,AM交DE于点F.
如图,已知△ABC,DE∥BC,交AB于点D,交AC于点E,点M在边BC上,AM交DE于点F.分析 (1)利用DE∥BC可判断△ADF∽△ABM,△AEF∽△AMC,则利用相似三角形的性质得$\frac{DF}{BM}$=$\frac{AF}{AM}$,$\frac{EF}{MC}$=$\frac{AF}{AM}$,所以$\frac{DF}{BM}$=$\frac{EF}{MC}$,然后利用比例性质即可得到结论;
(2)利用BM=CM和(1)中的结论可得到DF=EF;
(3)取AC的中点N,连结MN,BN,BN交AM于F′,如图,证明△ADE∽△ABC和△ADF∽△ABM可得到$\frac{AF}{AM}$=$\frac{AD}{AB}$=$\frac{2}{3}$,则$\frac{AF}{FM}$=2,再利用MN为△ABC的中位线和△F′AB∽△F′MN可得到$\frac{AF′}{F′M}$=$\frac{AB}{MN}$2,所以点F′与点F重合,由于点F′为△ABC的重心,于是可判断点F是△ABC的重心.
解答 (1)证明:∵DE∥BC,
∴△ADF∽△ABM,△AEF∽△AMC,
∴$\frac{DF}{BM}$=$\frac{AF}{AM}$,$\frac{EF}{MC}$=$\frac{AF}{AM}$,
∴$\frac{DF}{BM}$=$\frac{EF}{MC}$,
∴$\frac{DF}{EF}$=$\frac{BM}{MC}$;
(2)解:DF=EF.理由如下:
∵M是BC的中点,
∴BM=CM,
而$\frac{DF}{EF}$=$\frac{BM}{MC}$,
∴DF=EF;
(3)解:取AC的中点N,连结MN,BN,BN交AM于F′,如图,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{2}{3}$,
∵∴△ADF∽△ABM,
∴$\frac{AF}{AM}$=$\frac{AD}{AB}$=$\frac{2}{3}$,
∴$\frac{AF}{FM}$=2,
∵M点BC的中点,N点为AC的中点,
∴MN为△ABC的中位线,
∴MN∥AB,MN=$\frac{1}{2}$AB,
∵△F′AB∽△F′MN,
∴$\frac{AF′}{F′M}$=$\frac{AB}{MN}$2,
∴点F′与点F重合,
而点F′为△ABC的重心,
∴点F是△ABC的重心.
点评 本题考查了相似形综合题:熟练掌握相似三角形的判定与性质和三角形中位线的性质;解决问题的关键是熟练运用比例的性质.


科目:初中数学 来源: 题型:选择题
| A. | 320米 | B. | 320厘米 | C. | 2000厘米 | D. | 2000米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或-2 | B. | $\frac{1}{2}$或3 | C. | $\frac{1}{3}$或3 | D. | $\frac{1}{3}$或2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形OABC中,OA=4,OC=8,点D是线段OB的中点,点P从点A出发,以每秒1个单位的速度沿射线AO作匀速运动,点Q从点O出发,以每秒2个单位的速度沿x轴正半轴作匀速运动,P,Q同时出发,设运动的时间为t.
如图,矩形OABC中,OA=4,OC=8,点D是线段OB的中点,点P从点A出发,以每秒1个单位的速度沿射线AO作匀速运动,点Q从点O出发,以每秒2个单位的速度沿x轴正半轴作匀速运动,P,Q同时出发,设运动的时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
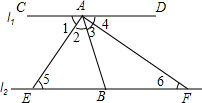 如图,已知直线l1∥直线l2,AE为∠CAB的角平分线,AF为∠DAB的角平分线,试说明:EB=BF.
如图,已知直线l1∥直线l2,AE为∠CAB的角平分线,AF为∠DAB的角平分线,试说明:EB=BF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△PQR是△ABC经过某种变换后得到的图形,如果△ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标为( )
如图,△PQR是△ABC经过某种变换后得到的图形,如果△ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标为( )| A. | (-a,b) | B. | (a,-b) | C. | (-a,-b) | D. | (-b,-a) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com