
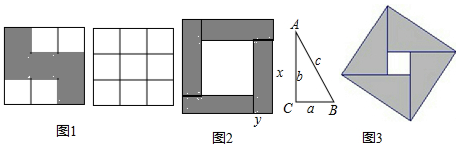
分析 (1)根据正方形的面积求出边长,即可得解;
(2)大正方形的面积减去矩形的面积即可得出阴影部分的面积,也可得出三个代数式x+y、x-y、xy之间的等量关系.
(3)先表示出中间小正方形的边长,然后根据大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积列出等式,然后整理即可得解.
解答 解:(1)如图1所示: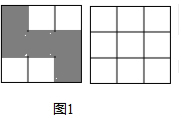
(2)代数式x+y、x-y、xy三者之间存在着等式关系:(x+y)2-4xy=(x-y)2;
(3)它能说明的等式为:c2=a2+b2.
推导如下:中间小正方形的边长为(b-a),
∴大正方形的面积可表示为:
c2=4×$\frac{1}{2}$ab+(b-a)2,
整理得,c2=2ab+b2-2ab+a2,
即c2=a2+b2.
故答案为:$\sqrt{5}$;(x+y)2-4xy=(x-y)2.
点评 本题考查了图形的剪拼,主要利用了正方形的面积,勾股定理,根据面积求出边长,再利用勾股定理作出相应边长的正方形即可,灵活掌握并运用网格结构是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
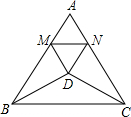 如图,△ABC是边长为5的等边三角形,△BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的∠MDN,点M、N分别在AB、AC上,连接MN,则△AMN的周长为5.
如图,△ABC是边长为5的等边三角形,△BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的∠MDN,点M、N分别在AB、AC上,连接MN,则△AMN的周长为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
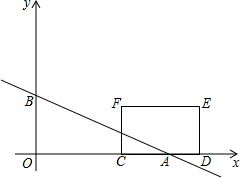 如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{3}$x+b(b>0),分别交x轴、y轴于A、B两点,点C(3,0),D(6,0),以CD为一边在x轴上方作矩形CDEF,CF=$\sqrt{3}$,设矩形CDEF与△ABO重叠部分的面积为S.
如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{3}$x+b(b>0),分别交x轴、y轴于A、B两点,点C(3,0),D(6,0),以CD为一边在x轴上方作矩形CDEF,CF=$\sqrt{3}$,设矩形CDEF与△ABO重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 三角形个数 | 1 | 2 | 3 | 4 |
| 火柴棒根数 | 3 | 5 | 7 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
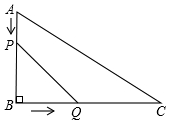 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问:
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com