
【题目】定义:对于任何数a,符号[a]表示不大于a的最大整数.
例如:[5.7]=5,[5]=5,[﹣1.5]=﹣2.
(1)[﹣![]() ]= ;
]= ;
(2)如果[a]=3,那么a的取值范围是 ;
(3)如果[![]() ]=﹣3,求满足条件的所有整数x.
]=﹣3,求满足条件的所有整数x.
科目:初中数学 来源: 题型:
【题目】小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
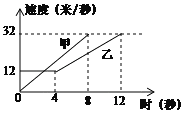
A. 乙前4秒行驶的路程为48米 B. 两车到第3秒时行驶的路程相等
C. 在0到8秒内甲的速度每秒增加4米/秒 D. 在4至8秒内甲的速度都大于乙的速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于点C,点D在抛物线上且横坐标为3.
(1)求A、B、C、D的坐标;
(2)求∠BCD的度数;
(3)求tan∠DBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求证:AE是⊙O的切线;
(2)当BC=4时求劣弧AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市在创建文明城区的活动中,有两个长度相等的彩色砖道铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设的彩色砖道的长度y(米)与施工时间x(小时)之间关系的部分图象,请解答下列问题:
(1)求乙队在0≤x≤6的时段内y与x的函数关系式.
(2)如果甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/小时,结果两队同时完成了任务,求甲队从开始施工到完成所铺设的彩色砖道的长度为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
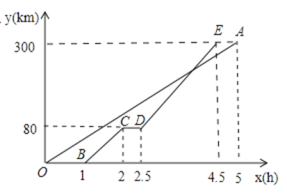
【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发驶向乙地。如图,线段OA表示货车离甲地的距离![]() (km)与时间
(km)与时间![]() (h)之间的函数关系,折线BCDE变式轿车离甲地的距离
(h)之间的函数关系,折线BCDE变式轿车离甲地的距离![]() (km)与时间
(km)与时间![]() (h)之间的函数关系。根据图像,解答下列问题:
(h)之间的函数关系。根据图像,解答下列问题:
(1)线段CD表示轿车在途中停留了 h.
(2)求线段DE对应的函数关系式(2.5≤x≤4.5).
(3)求轿车从甲地出发后经过多长时间追上货车.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com