
ČēĶ¼£¬ŅŃÖŖµćA(−3£¬5)ŌŚÅ×ĪļĻßy= x2+cµÄĶ¼ĻóÉĻ£¬µćP“ÓÅ×ĪļĻߵĶ„µćQ³ö·¢£¬ŃŲyÖįŅŌ
x2+cµÄĶ¼ĻóÉĻ£¬µćP“ÓÅ×ĪļĻߵĶ„µćQ³ö·¢£¬ŃŲyÖįŅŌ
ĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÕż·½ĻņŌĖ¶Æ£¬Į¬½įAP²¢ŃÓ³¤£¬½»Å×ĪļĻßÓŚµćB£¬·Ö±š¹żµćA”¢B×÷xÖįµÄ“¹Ļߣ¬“¹
×ćĪŖC”¢D£¬Į¬½įAQ”¢BQ£®
(1)ĒóÅ×ĪļĻߵĽāĪöŹ½£»
(2)µ±A”¢Q”¢BČżµć¹¹³ÉŅŌAQĪŖÖ±½Ē±ßµÄÖ±½ĒČż½ĒŠĪŹ±£¬ĒóµćPĄėæŖµćQ¶ąÉŁŹ±¼ä£æ
(3)ŹŌĢ½Ė÷µ±AP”¢AC”¢BP”¢BDÓėŅ»øöĘ½ŠŠĖıߊĪµÄĖÄĢõ±ß¶ŌÓ¦ĻąµČ£Ø¼“ÕāĖÄĢõĻ߶ĪÄܹ¹³ÉĘ½ŠŠĖıߊĪ£©Ź±£¬µćPĄėæŖµćQµÄŹ±æĢ£®

£Ø1£©°ŃA£Ø−3£¬5£©“śČėµĆ£ŗ5= ´9+c£¬
´9+c£¬
”ąc= £®
£®
£Ø2£©¢ŁČōAQ”ĶBQ£¬¹żµćQ×÷MN”ĶyÖį£¬

æÉÖ¤”÷AMQ”×”÷QNB£®
”ßAM=AC−MC= £¬MQ=3£¬
£¬MQ=3£¬
”ą £®
£®
ÉčB£Ø3k£¬2k+ £©£¬
£©£¬
“śČėÅ×ĪļĻß½āĪöŹ½µĆ£ŗk= £¬¼“B£Ø
£¬¼“B£Ø £¬
£¬ £©£®
£©£®
”ąÖ±ĻßABµÄ½āĪöŹ½ĪŖ£ŗ £®
£®
”ąOP=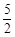 £¬”ąPQ=2£®
£¬”ąPQ=2£®
¢ŚČōAQ”ĶAB£¬

”ßAC”ĪPQ£¬æÉÖ¤”÷AMQ”×”÷QAP£¬
ÓÖÓɹ“¹É¶ØĄķµĆAQ= £®
£®
”ąPQ= £®
£®
”ą¶ŌÓ¦µÄŹ±æĢtĪŖ£ŗ2»ņ £®
£®
£Ø3£©¢ŁČōAC=BD£¬AP=BP£¬
“ĖŹ±µćAÓėµćB¹ŲÓŚyÖį¶Ō³Ę£¬
”ąOP=AC=5£¬
”ąPQ=4 £®
£®
¢ŚČōAC=AP£¬
ÉčP£Ø0£¬y£©£¬Ōņ£ŗ9+(y−5)2=25£¬
½āÖ®µĆ£¬y=1£¬¼“OP=1£®
”ąPQ= £®
£®
“ĖŹ±£¬Ö±ĻßAP½āĪöŹ½ĪŖ£ŗ £®
£®
ÓėÅ×ĪļĻߵĽ»µćBĪŖ£Ø £¬
£¬ £©£¬
£©£¬
”ąPB= =BD£®
=BD£®
”ąĀś×ćĢõ¼žµÄŹ±æĢĪŖ£ŗ ŗĶ4
ŗĶ4 £®
£®
”¾½āĪö”æ£Ø1£©°ŃAµć×ų±ź“śČė¾ĶµĆµ½Å×ĪļĻߵĽāĪöŹ½£»
£Ø2£©·ÖAQ”ĶBQ, AQ”ĶABĮ½ÖÖĒéæö½ųŠŠĢÖĀŪ£»
£Ø3£©·ÖAC=BD”¢AC=APĮ½ÖÖĒéæö½ųŠŠĢÖĀŪ”£


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 16”¢ČēĶ¼£¬ŅŃÖŖµćDŹĒ”ĻABCµÄĘ½·ÖĻßÉĻŅ»µć£¬µćPŌŚBDÉĻ£¬PA”ĶAB£¬PC”ĶBC£¬“¹×ć·Ö±šĪŖA£¬C”¢ĻĀĮŠ½įĀŪ“ķĪóµÄŹĒ£Ø””””£©
16”¢ČēĶ¼£¬ŅŃÖŖµćDŹĒ”ĻABCµÄĘ½·ÖĻßÉĻŅ»µć£¬µćPŌŚBDÉĻ£¬PA”ĶAB£¬PC”ĶBC£¬“¹×ć·Ö±šĪŖA£¬C”¢ĻĀĮŠ½įĀŪ“ķĪóµÄŹĒ£Ø””””£©²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
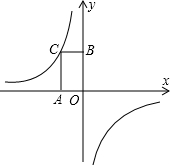 ČēĶ¼£¬ŅŃÖŖµćCĪŖ·“±ČĄżŗÆŹży=-
ČēĶ¼£¬ŅŃÖŖµćCĪŖ·“±ČĄżŗÆŹży=-| 6 | x |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼£¬ŅŃÖŖµćA”¢B”¢C”¢D¾łŌŚŅŃÖŖŌ²ÉĻ£¬AD”ĪBC£¬ACĘ½·Ö”ĻBCD£¬”ĻADC=120”ć£¬ĖıߊĪABCDµÄÖܳ¤ĪŖ10cm£®Ķ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ĪŖ£Ø””””£©
ČēĶ¼£¬ŅŃÖŖµćA”¢B”¢C”¢D¾łŌŚŅŃÖŖŌ²ÉĻ£¬AD”ĪBC£¬ACĘ½·Ö”ĻBCD£¬”ĻADC=120”ć£¬ĖıߊĪABCDµÄÖܳ¤ĪŖ10cm£®Ķ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ĪŖ£Ø””””£©A”¢
| ||||
BӢ
| ||||
CӢ2
| ||||
DӢ4
|
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼£¬ŅŃÖŖµćDĪŖ”÷ABCÖŠAC±ßÉĻŅ»µć£¬ĒŅAD£ŗDC=3£»4£¬Éč
ČēĶ¼£¬ŅŃÖŖµćDĪŖ”÷ABCÖŠAC±ßÉĻŅ»µć£¬ĒŅAD£ŗDC=3£»4£¬Éč| BA |
| a |
| BC |
| b |
| BD |
| a |
| b |
| a |
| b |
| BD |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼£¬ŅŃÖŖµćCĪŖABÉĻŅ»µć£¬AC=12cm£¬CB=
ČēĶ¼£¬ŅŃÖŖµćCĪŖABÉĻŅ»µć£¬AC=12cm£¬CB=| 2 | 3 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com