
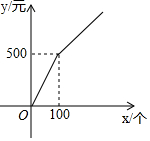
 ij��������������һ��С��Ʒ��ÿ���ۼ�mԪ�����һ�ι���100�����ϣ�����100���IJ����ۼ۴�8�ۣ�������y��Ԫ���빺������x������֮��Ĺ�ϵ��ͼ��ʾ�����������ϰ彫ijһ�������������Ƴ���ͼ��ʾ�ı���
ij��������������һ��С��Ʒ��ÿ���ۼ�mԪ�����һ�ι���100�����ϣ�����100���IJ����ۼ۴�8�ۣ�������y��Ԫ���빺������x������֮��Ĺ�ϵ��ͼ��ʾ�����������ϰ彫ijһ�������������Ƴ���ͼ��ʾ�ı���| ��������x������ | 60 | 100 | 120 | 200 | c |
| ������y��Ԫ�� | a | 500 | 580 | b | 1500 |
���� ��1���ٵ�0��x��100ʱ����y=kx���ڵ�x��100ʱ����y=k��x+b�䣬�ֱ����ô���ϵ�������ɽ�����⣻
��2�����ã�1���еĺ�����ϵʽ���������ֵ���Ա�����ֵ���ɣ�
��3�����������Σ��������֮�ͼ��ɣ�
��� �⣺��1���ٵ�0��x��100ʱ��
��y=kx����x=100��y=500���룬�ɵ�k=5��
��y=5x��
�ڵ�x��100ʱ����y=k��x+b�䣬������$\left\{\begin{array}{l}{100k��+b��=500}\\{120k��+b��=580}\end{array}\right.$��
���$\left\{\begin{array}{l}{k��=4}\\{b��=100}\end{array}\right.$��
��y=4x+100��
����������y=$\left\{\begin{array}{l}{5x}&{��0��x��100��}\\{4x+100}&{��x��100��}\end{array}\right.$
��2��m=$\frac{500}{100}$=5��a=5��60=300��b=4��200+100=900��
1500=4c+100��c=350��
�ʴ�Ϊ5��300��900��350��
��3����������һ������õ�����Ϊ160����5-2��+670����4-2��=2490Ԫ��
���� ���⿼��һ�κ�����Ӧ�á�����ϵ���������������������ۡ����ۼ�֮��Ĺ�ϵ��֪ʶ������Ĺؼ��Ƕ���ͼ����Ϣ�����������ѧ֪ʶ������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ȡǰ100��ѧ���ijɼ� | B�� | ��ȡ��100��ѧ���ijɼ� | ||
| C�� | ��ȡ��1����2���������ѧ���ɼ� | D�� | ��ȡѧ��Ϊ4�ı�����ѧ���ijɼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
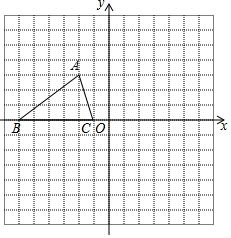 ��ͼ����֪��ABC��������������ΪA��-2��3����B��-6��0����C��-1��0����
��ͼ����֪��ABC��������������ΪA��-2��3����B��-6��0����C��-1��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com