
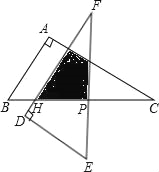
【题目】如图△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.
(1)PH=_____cm.
(2)△ABC与△DEF重叠部分的面积为_____cm2.
【答案】![]()
![]()
【解析】
如图,由点P为斜边BC的中点得到PC=![]() BC=6,再根据旋转的性质得PF=PC=6,∠FPC=90°,∠F=∠C=30°,根据含30度的直角三角形三边的关系,在Rt△PFH中计算出PH=
BC=6,再根据旋转的性质得PF=PC=6,∠FPC=90°,∠F=∠C=30°,根据含30度的直角三角形三边的关系,在Rt△PFH中计算出PH=![]() PF=2
PF=2![]() ;在Rt△CPM中计算出PM=
;在Rt△CPM中计算出PM=![]() PC=2
PC=2![]() ,且∠PMC=60°,则∠FMN=∠PMC=60°,于是有∠FNM=90°,FM=PF-PM=6-2
,且∠PMC=60°,则∠FMN=∠PMC=60°,于是有∠FNM=90°,FM=PF-PM=6-2![]() ,则在Rt△FMN中可计算出MN=
,则在Rt△FMN中可计算出MN=![]() FM=3-
FM=3-![]() ,FN=
,FN=![]() MN=3
MN=3![]() -3,然后根据三角形面积公式和利用△ABC与△DEF重叠部分的面积=S△FPH-S△FMN进行计算即可.
-3,然后根据三角形面积公式和利用△ABC与△DEF重叠部分的面积=S△FPH-S△FMN进行计算即可.
解:如图,
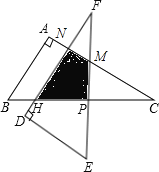
∵点P为斜边BC的中点,
∴PB=PC=![]() BC=6,
BC=6,
∵△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,
∴PF=PC=6,∠FPC=90°,∠F=∠C=30°,
在Rt△PFH中,∵∠F=30°,
∴PH=![]() PF=2
PF=2![]() ,
,
在Rt△CPM中,∵∠C=30°,
∴PM=![]() PC=2
PC=2![]() ,∠PMC=60°,
,∠PMC=60°,
∴∠FMN=∠PMC=60°,
∴∠FNM=90°,
∴FM=PF-PM=6-2![]() ,
,
在Rt△FMN中,∵∠F=30°,
∴MN=![]() FM=3-
FM=3-![]() ,
,
∴FN=![]() MN=3
MN=3![]() -3,
-3,
∴△ABC与△DEF重叠部分的面积=S△FPH-S△FMN
=![]() ,
,
=9(cm2).
故答案为:![]() ; 9.
; 9.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】阅读下列题目的解题过程:
已知![]() 为
为![]() 的三边,且满足
的三边,且满足![]() ,试判断
,试判断![]() 的形状.
的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴![]() 是直角三角形
是直角三角形
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号: ;
(2)该步正确的写法应是: ;
(3)本题正确的结论为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
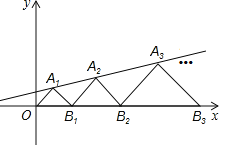
【题目】如图,在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=![]() x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2018的纵坐标是_____.
x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2018的纵坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
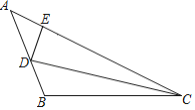
【题目】如图,在△ABC中,∠B>90°,CD为∠ACB的角平分线,在AC边上取点E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,则( )
A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣![]() β
β
C.∠AED=90°﹣α+βD.∠AED=90°+α+![]() β
β
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形并解答有关问题.
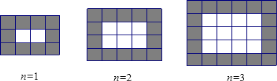
![]() 在第n个图中,第一横行共______ 块瓷砖,第一竖列共有______ 块瓷砖;
在第n个图中,第一横行共______ 块瓷砖,第一竖列共有______ 块瓷砖;![]() 均用含n的代数式表示
均用含n的代数式表示![]()
![]() 设铺设地面所用瓷砖的总块数为y,请写出y与
设铺设地面所用瓷砖的总块数为y,请写出y与![]() 中的n的函数;
中的n的函数;
![]() 按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值;
按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值;
![]() 是否存在黑瓷砖与白瓷砖块数相等的情形请通过计算说明理由.
是否存在黑瓷砖与白瓷砖块数相等的情形请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船自西向东航行,在![]() 处测得东偏北
处测得东偏北![]() 方向有一座小岛
方向有一座小岛![]() ,继续向东航行
,继续向东航行![]() 海里到达
海里到达![]() 处,测得小岛
处,测得小岛![]() 此时在轮船的东偏北
此时在轮船的东偏北![]() 方向上.之后,轮船继续向东航行多少海里,距离小岛
方向上.之后,轮船继续向东航行多少海里,距离小岛![]() 最近?(参考数据:
最近?(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两车间接到加工一批零件的任务,从开始加工到完成这项任务共用了9天,乙车间在加工2天后停止加工,引入新设备后继续加工,直到与甲车间同时完成这项任务为止,设甲、乙车间各自加工零件总数为y(件),与甲车间加工时间x(天),y与x之间的关系如图(1)所示.由工厂统计数据可知,甲车间与乙车间加工零件总数之差z(件)与甲车间加工时间x(天)的关系如图(2)所示.
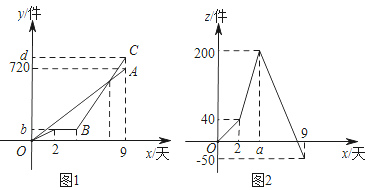
(1)甲车间每天加工零件为_____件,图中d值为_____.
(2)求出乙车间在引入新设备后加工零件的数量y与x之间的函数关系式.
(3)甲车间加工多长时间时,两车间加工零件总数为1000件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com