

分析 (1)由内角和定理得∠BAC=70°,由角平分线性质得∠EAC=35°,再根据直角三角形的性质可得∠DAC=15°,从而由∠EAD=∠EAC-∠DAC可得答案;
(2)由AE平分∠BAC得∠BAE=$\frac{1}{2}$∠BAC,由∠BAC=180°-∠B-∠C得∠EAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C,根据∠EAD=∠EAC-∠DAC可得答案;
(3)AG⊥BC于G,则FD∥AG可得∠EFD=∠EAG,由(2)知∠EAG=$\frac{1}{2}$(∠C-∠B),即可得答案;
(4)作AG⊥BC于G,与(3)同理.
解答 解:(1)∵∠C=75°,∠B=35°,
∴∠BAC=180°-∠C-∠B=70°,
∵AE平分∠BAC,
∴∠EAC=$\frac{1}{2}$∠BAC=35°,
又∵AD⊥BC,
∴∠DAC=90°-∠C=15°,
则∠EAD=∠EAC-∠DAC=20°;
(2)∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC,
∵∠BAC=180°-∠B-∠C,
∴∠EAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C,
∴∠EAD=∠EAC-∠DAC=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C-(90°-∠C)=$\frac{1}{2}$(∠C-∠B);
(3)如图②,过A作AG⊥BC于G,由(2)知,∠EAG=$\frac{1}{2}$(∠C-∠B),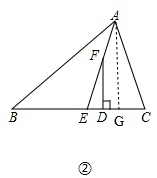
∵AG⊥BC,
∴∠AGC=90°,
∵FD⊥BC,
∴∠FDG=90°,
∴∠AGC=∠FDG,
∴FD∥AG,
∴∠EFD=∠EAG,
∴∠EFD=$\frac{1}{2}$(∠C-∠B),
故答案为:∠EFD=$\frac{1}{2}$(∠C-∠B);
(4)如图③,过A作AG⊥BC于G,由(1)知,∠EAG=$\frac{1}{2}$(∠C-∠B),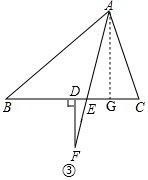
∵AG⊥BC,
∠AGB=90°,
∵FD⊥BC,
∴∠FDC=90°,
∴∠AGC=∠FDC,
∴FD∥AG,
∴∠AFD=∠EAG,
∴∠AFD=$\frac{1}{2}$(∠C-∠B),
故答案为:∠AFD=$\frac{1}{2}$(∠C-∠B).
点评 本题主要考查三角形的内角和定理、角平分线的性质、直角三角形的性质和平行线的判定与性质,熟练掌握三角形的内角和定理和角平分线的性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
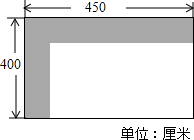 小明家想要在自己家的阳台上铺地砖,经测量后设计了如图的图纸,黑色区域为宽度相等的一条“7”形的健身用鹅卵石小路,空白部分为地砖铺设区域.要使铺地砖的面积为14平方米,那么小路的宽度应为0.5米.
小明家想要在自己家的阳台上铺地砖,经测量后设计了如图的图纸,黑色区域为宽度相等的一条“7”形的健身用鹅卵石小路,空白部分为地砖铺设区域.要使铺地砖的面积为14平方米,那么小路的宽度应为0.5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com