
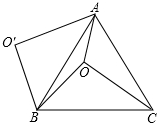
 如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$
如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 证明△BO′A≌△BOC,又∠OBO′=60°,所以△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;由△OBO′是等边三角形,可知结论②正确;在△AOO′中,三边长为6,8,10,这是一组勾股数,故△AOO′是直角三角形;进而求得∠AOB=150°,故结论③正确;S四边形AOBO′=S△AOO′+S△OBO可对称④作出判断.
解答 解:由题意可知,∠1+∠2=∠3+∠2=60°,
∴∠1=∠3.
又∵OB=O′B,AB=BC,
∴△BO′A和△BOC中$\left\{\begin{array}{l}{OB=O′B}\\{∠1=∠3}\\{AB=BC}\end{array}\right.$.
∴△BO′A≌△BOC(SAS).
又∵∠OBO′=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到.
故结论①正确;
如图所示:连接OO′.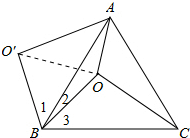
∵OB=O′B,且∠OBO′=60°,
∴△OBO′是等边三角形,
∴OO′=OB=8.
故结论②正确;
∵△BO′A≌△BOC,
∴O′A=10.
在△AOO′中,三边长为6,8,10,这是一组勾股数,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故结论③正确;
S四边形AOBO′=S△AOO′+S△OBO′=$\frac{1}{2}$×6×8+$\frac{1}{2}$×8×$4\sqrt{3}$=24+16$\sqrt{3}$,故结论④错误.
综上所述,正确的结论为:①②③.
故选:B.
点评 本题考查了旋转变换中等边三角形,直角三角形的性质.利用勾股定理的逆定理,判定勾股数6、10、10所构成的三角形是直角三角形是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.1×10-9m | B. | 8.1×10-8m | C. | 81×10-9m | D. | 0.81×10-7m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≠5 | B. | x≠3 | C. | x≥3 | D. | x≥3 且 x≠5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com