
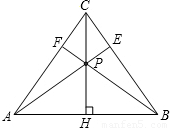
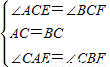 ,
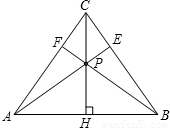
,
 ∠C,而∠CAE<∠CAH,要使AE=AC,只需使∠C=∠CEA,
∠C,而∠CAE<∠CAH,要使AE=AC,只需使∠C=∠CEA,

 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源:2010年广东省广州市南沙区中考数学一模试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2009年重庆市綦江县赶水中学学模拟测试数学试卷(解析版) 题型:解答题
 ∠β.(只须作出正确图形,保留作图痕迹,不必写出作法)
∠β.(只须作出正确图形,保留作图痕迹,不必写出作法)
查看答案和解析>>
科目:初中数学 来源:2009年浙江省嘉兴市数学素质评估卷3(秀洲区王江泾镇中学)(解析版) 题型:选择题
 ,S2=
,S2=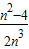 ,…;记W=S1+S2+…+Sn-1,当n越来越大时,你猜想W最接近的常数是( )
,…;记W=S1+S2+…+Sn-1,当n越来越大时,你猜想W最接近的常数是( )




查看答案和解析>>
科目:初中数学 来源:2008年浙江省杭州市中考数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com