
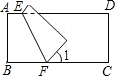
 如图,把长方形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF=
如图,把长方形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF=科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013届江苏省江阴市长泾片九年级上学期期末考试数学试卷(带解析) 题型:解答题
【问题提出】我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
【问题解决】如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.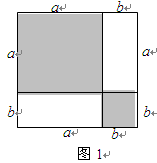
解:由图可知: ,
, .
.
∴ .
.
∵a≠b,∴ >0.
>0.
∴M-N>0.∴M>N.
【类比应用】(1)已知:多项式M =2a2-a+1 ,N =a2-2a .
试比较M与N的大小.
(2)已知:如图2,锐角△ABC (其中BC为a ,AC为 b,
AB为c)三边满足a <b < c ,现将△ABC 补成长方形,
使得△ABC的两个顶点为长方形的两个端点,第三个顶点落
在长方形的这一边的对边上。
①这样的长方形可以画 个;
②所画的长方形中哪个周长最小?为什么?
【拓展延伸】 已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边满足a <b < c ,画其BC边上的内接正方形EFGH , 使E、F两点在边BC上,G、H分别在边AC、AB上,同样还可画AC、AB边上的内接正方形,问哪条边上的内接正方形面积最大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
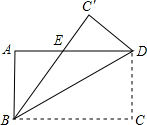
 如图,把长方形ABCD(AB=CD,AD=BC,∠A=∠ABC=∠C=∠CDA=90°)沿对角线BD对折,使点C落在点C,处,请说明AE=C′E.
如图,把长方形ABCD(AB=CD,AD=BC,∠A=∠ABC=∠C=∠CDA=90°)沿对角线BD对折,使点C落在点C,处,请说明AE=C′E.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com