Question

10．如图：在△ABC中，∠ACB=90°，∠B=30°，AC=1，AC在直线l上，将△ABC绕点A顺时针旋转到位置①，可得到点P₁，此时AP₁=2；将位置①的三角形绕点P₁顺时针旋转到位置②，可得到点P₂，此时AP₂=2+$\sqrt{3}$；将位置②的三角形绕点P₂顺时针旋转到位置③，可得到点P₃，可得到点P₃，此时AP₃=3+$\sqrt{3}$；…，按此规律继续旋转，直到得到点P₂₀₁₅为止，则AP₂₀₁₅=（　　）

• A． 2015+672$\sqrt{3}$
• B． 2013+671$\sqrt{3}$
• C． 2013+672$\sqrt{3}$
• D． 2015+671$\sqrt{3}$

Answer 1

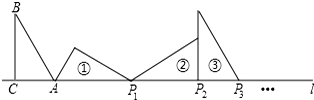
分析 先求出△ABC三边的长，再依次计算AP₁、AP₂、AP₃、…，发现每旋转三次时，A到P的距离为三角形的周长，增加一次，长度增加2，增加2次时，长度增加2+$\sqrt{3}$，增加3时，长度增加周长3+$\sqrt{3}$；因此要计算AP₂₀₁₅=的长度，要先计算2015除以3，商是多少，余数是多少，从而得出结果．

解答 解：在Rt△ABC中，
∵∠B=30°，AC=1，
∴AB=2，BC=$\sqrt{3}$，
由旋转得：AP₁=AB=2，
AP₂=AP₁+P₁P₂=2+$\sqrt{3}$，
AP₃=AP₁+P₁P₂+P₂P₃=3+$\sqrt{3}$，
…
∵2015÷3=671…2，
∴AP₂₀₁₅=671（3+$\sqrt{3}$）+2+$\sqrt{3}$=2015+672$\sqrt{3}$，
故选A．

点评 本题是旋转变换问题，也是图形类规律问题；考查了含30°角的直角三角形的性质和勾股定理，此类题的解题思路为：①先表示出直角三角形各边长；②因为要计算AP₂₀₁₅的长，所以从AP₁、AP₂、AP₃、依次计算，并总结规律，如果看不出可以多计算几个长度．