
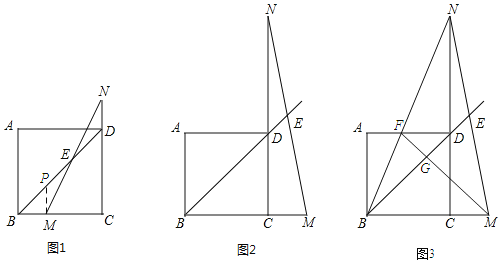
【题目】在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN,直线BD与MN交于点E.
(1)如图1.当点M在BC上时,为证明“BD﹣2DE=![]() BM”这一结论,小敏添加了辅助线:过点M作CD的平行线交BD于点P.请根据这一思路,帮助小敏完成接下去的证明过程.
BM”这一结论,小敏添加了辅助线:过点M作CD的平行线交BD于点P.请根据这一思路,帮助小敏完成接下去的证明过程.
(2)如图2,当点M在BC的延长线上时,则BD,DE,BM之间满足的数量关系是 .
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G,如图3,若![]() CM=2,则线段DG= .
CM=2,则线段DG= .
【答案】(1)见解析;(2)BD+2DE=![]() BM;(3)
BM;(3)![]() .
.
【解析】
(1)过点M作MP∥CD,交BD于点P,推出PM=DN,证明△EPM≌△EDN,推出EP=ED,根据正方形的性质和勾股定理求出即可;
(2)过点M作MP∥CD交BD的延长线于点P,推出BM=PM=DN,根据AAS证明△EPM≌△EDN,推出EP=ED,根据正方形的性质和勾股定理求出即可;
(3)证明△ABF∽△DNF,得出比例式,得到AB:ND=1:2,设AB=x,则DN=2x,
根据BM=DN,列出方程求出AB的长度,根据DF∥BM,得到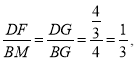 即可求解.
即可求解.
解:(1)如图1,过点M作MP∥CD,交BD于点P,
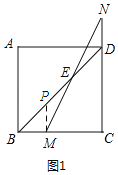
∵四边形ABCD是正方形,
∴∠C=90°,∠CBD=∠CDB=45°,
∵PM∥CD,
∴∠NDE=∠MPE,∠BPM=∠CDB=45°,
∴△BPM是等腰直角三角形,
∴PM=BM,![]()
∵BM=DN,
∴PM=DN,
在△EPM和△EDN中,
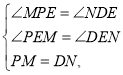
∴△EPM≌△EDN(AAS),
∴EP=ED,
∴PB=BD﹣PD=BD﹣2DE,
根据勾股定理得:![]()
即![]()
(2)如图2,过点M作MP∥CD交BD的延长线于点P,

∴∠PMB=∠BCD=90°,
∵∠CBD=45°,
∴△BMP是等腰直角三角形,
∴BM=PM=DN,
与(1)证法类似:△EPM≌△EDN(AAS),
∴EP=ED,
∴PB=BD+PD=BD+2DE,
根据勾股定理得:BP=![]() BM,
BM,
即BD+2DE=BP=![]() BM,
BM,
故答案为:BD+2DE=![]() BM;
BM;
(3)如图3,∵
∴AB∥DN,

∴△ABF∽△DNF,
∴AF:FD=AB:ND,
∵AF:FD=1:2,
∴AB:ND=1:2,
设AB=x,则DN=2x,
∵BM=DN,
∴x+2=2x,x=2,
∴AB=AD=2,DF=![]() ,
,
∴![]()
∵DF∥BM,
∴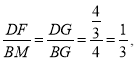
∴![]()
故答案为:![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙、丙3人聚会,每人带了一件礼物,3件礼物从外盒包装看完全相同,里面的东西只有颜色不同,将3件礼物放在一起.
(1)甲从中随机抽取一件,求甲抽到不是自己带来的礼物的概率;
(2)每人从中随机抽取一件,求甲、乙、丙3人抽到的都不是自己带来的礼物的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①.抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于A(﹣1,0)、B(3,0)、C三点.
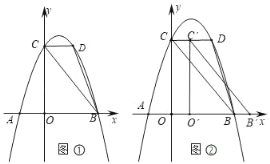
(1)求a和b的值;
(2)点D(2,m)在第一象限的抛物线上,连接BC、BD、CD,在对称轴左侧的抛物线上存在一点P,满足∠PBC=∠DBC,请求出点P的坐标;
(3)如图②,在(2)的条件下将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B'O'C'在平移过程中,△B'O'C'与△BCD重叠部分的面积记为S,设平移的时问为t秒,请直接写出S与t之间的函数关系式(并注明自变量的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次大课间活动中,采用了四种活动形式:A:跑步;B:跳绳;C:做操;D:游戏,全校学生都选择了一种形式参与活动,小明对同学们选择的活动形式进行了随机抽样调查,并绘制了不完整的两幅统计图(如图):
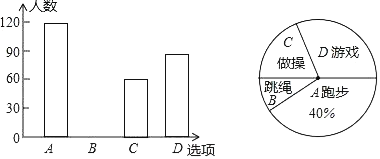
(1)本次共调查了多少名学生?
(2)跳绳B对应扇形的圆心角为多少度?
(3)学校在每班A、B、C、D四种活动形式中,随机抽取两种开展活动,求每班抽取的两种形式恰好是“做操”和“跳绳”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
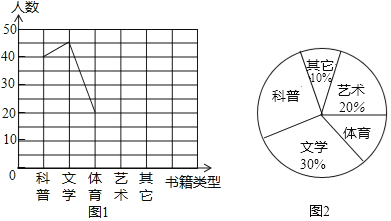
【题目】“腹有诗书气自华,阅读路伴我成长”,我区某校学生会以“每天阅读1小时”为问卷主题,对学生最喜爱的书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅末完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)把折线统计图(图1)补充完整;
(2)该校共有学生1200名,请估算最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克 40 元,规定每千克售价不低于成本,且不高于 80 元,经市场调查,每天的销售量 y( 千克)与每千克售价x(元)满足一次函数关系,部分数据如表:

(1)求 y 与 x 之间的函数表达式;
(2)设商品每天的总利润为 W(元),求 W 与 x 之间的函数表达式(利润=收入﹣成本);
(3)指出售价为多少元时获得利润最大?并试说明(2)中总利润W随售价x的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
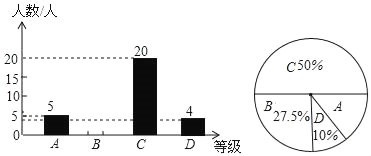
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2-2x-1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
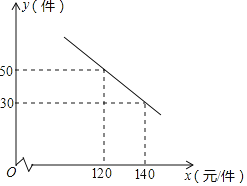
【题目】某商场购进一种每件价格为90元的新商品,在商场试销时发现:销售单价![]() 元
元![]() 件
件![]() 与每天销售量
与每天销售量![]() 件
件![]() 之间满足如图所示的关系.
之间满足如图所示的关系.
![]() 求出y与x之间的函数关系式;
求出y与x之间的函数关系式;
![]() 写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com