
【题目】图中的数阵是由全体正奇数排成的.
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在图中任意作一个类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由.这九个数之和能等于2 016吗?2 015,2 025呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.

【答案】(1)平行四边形框内的九个数之和是中间的数的9倍.(2)这九个数之和不能为2016;这九个数之和也不能为2015;这九个数之和能为2025,中间数为225,最小的数为207.
【解析】
(1)、求出各数与中间数的差值,观察发现该值成对出现,此时不难得到这九个数之和与中间数的关系了;
(2)、不妨设框中间的数为n,根据(1)中各数与中间数的关系,可用n表示出各数,从而得到9个数之和与中间数的关系;
由上面的结果不难得到任意作一个类似(1)的平行四边形框,框中的九个数之和都是中间的数的9倍,从而判断出2015、2016、2025中可能是这九个数之和的数.注意:数阵是由全体奇数排成!
最后,根据框中的最小的数比中间的数小18,即可得到九个数中最小的一个.
(1)平行四边形框内的九个数之和是中间的数的9倍.
(2)任意作一个类似(1)中的平行四边形框,规律仍然成立.
不妨设平行四边形框中间的数为n,则这九个数按从小到大的顺序排列依次为(n-18),(n-16),(n-14),(n-2),n,(n+2),(n+14),(n+16),(n+18).显然,其和为9n,是n的9倍.
这九个数之和不能为2 016.若和为2 016,则9n=2 016,n=224,是偶数,显然不在数阵中.
这九个数之和也不能为2 015.因为2 015不能被9整除.
这九个数之和能为2 025,中间数为225,最小的数为225-18=207


科目:初中数学 来源: 题型:
【题目】“五一”小长假,小颖和小梅两家计划从“北京天安门”“三亚南山”“内蒙古大草原”三个景区中任意选择一景区游玩,小颖和小梅制作了如下三张质地大小完全相同的卡片,背面朝上洗匀后各自从中抽去一张来确定游玩景区(第一人抽完放回洗匀后另一人再抽去),则两人抽到同一景区的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知当x1=a,x2=b,x3=c时,二次函数y= ![]() x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y= ![]() (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3, ![]() ).
). 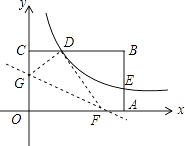
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD的对角线AC,BD相交于点O,AC=4 ![]() ,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1 , 未被盖住部分的面积为S2 , BP=x.
,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1 , 未被盖住部分的面积为S2 , BP=x. 
(1)用含x的代数式分别表示S1 , S2;
(2)若S1=S2 , 求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列做法正确的是( )
A. 方程![]() =1+
=1+![]() 去分母,得2(2x-1)=1+3(x-3)
去分母,得2(2x-1)=1+3(x-3)
B. 方程4x=7x-8移项,得4x-7x=8
C. 方程3(5x-1)-2(2x-3)=7去括号,得15x-3-4x-6=7
D. 方程1-![]() x=3x+
x=3x+![]() 移项,得-
移项,得-![]() x-3x=
x-3x=![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC三边长a=b=6![]() ,c=12.
,c=12.
(1)如图1,以点A为原点,AB所在直线为x轴建立平面直角坐标系,直接出点B,C的坐标.
(2)如图2,过点C作∠MCN=45°交AB于点M,N,请证明AM2+BN2=MN2;
(3)如图3,当点M,N分布在点B异侧时,则(3)中的结论还成立吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F. 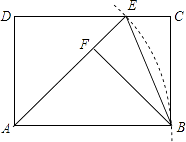
(1)求证:BF=AD;
(2)若EC= ![]() ﹣1,∠FEB=67.5°,求扇形ABE的面积(结果保留π).
﹣1,∠FEB=67.5°,求扇形ABE的面积(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com