
【题目】如图,平面直角坐标系中,已知点A(0,10),点B(m,10)在第一象限,连接AB、OB.
(1)如图1,若OB=12,求m的值.

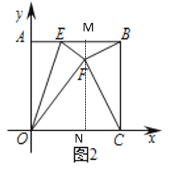
(2)如图2,当m=10时,过B作BC⊥x轴于C,E为AB边上一点,AE=![]() ,把△OAE沿直线OE翻折得到△OFE(点A的对应点为点F),连接BF、CF,求证:BF⊥CF.
,把△OAE沿直线OE翻折得到△OFE(点A的对应点为点F),连接BF、CF,求证:BF⊥CF.

(3)如图3,将△AOB沿直线OB翻折得到△GOB(点A的对应点为点G),若点G到x轴的距离不大于8,直接写出m的取值范围为 .

【答案】(1)m=![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() ≤m≤30
≤m≤30
【解析】
(1)根据勾股定理计算AB的长,可得m的值;
(2)过点F作FM⊥AB,延长MF交OC于点N,由折叠性质可知:EF=AE=![]() ,OF=OA=10,∠EFO=∠OAE=90°,然后根据正方形的性质和AA定理证得△EFM∽△FON,设FM=x,根据相似三角形的性质求得
,OF=OA=10,∠EFO=∠OAE=90°,然后根据正方形的性质和AA定理证得△EFM∽△FON,设FM=x,根据相似三角形的性质求得![]() ,然后利用勾股定理列方程求解x的值,从而求得MF=2,NF=8,ON=6,NC=4,然后再利用勾股定理求得
,然后利用勾股定理列方程求解x的值,从而求得MF=2,NF=8,ON=6,NC=4,然后再利用勾股定理求得![]() 、
、![]() ,
,![]() ,从而利用勾股定理逆定理判定△BCF是直角三角形,从而求解;
,从而利用勾股定理逆定理判定△BCF是直角三角形,从而求解;
(3)由条件可知点G的纵坐标大于或等于-8小于或等于8.分别计算点G的纵坐标为8和-8时m的值可得m的取值范围.
解:(1)由A(0,10),点B(m,10)可知AB⊥y轴,
∵OB=12,OA=10,
∴在Rt△AOB中,AB=![]() ,
,
∴m=![]() ;
;
(2)过点F作FM⊥AB,延长MF交OC于点N
由折叠性质可知:EF=AE=![]() ,OF=OA=10,∠EFO=∠OAE=90°
,OF=OA=10,∠EFO=∠OAE=90°
由题意可知,当m=10时,四边形AOCB是正方形且MN⊥AB
∴MN⊥OC
∴∠EMF=∠FNO=90°
又∵∠EFM+∠OFN=90°,∠OFN+∠FON=90°
∴∠EFM=∠FON
∴△EFM∽△FON
设FM=x,则FN=10-x
∴![]() ,即
,即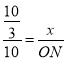 ,解得:
,解得:![]()
∴在Rt△FON中,![]()
解得:x=0(舍去)或x=2
∴MF=2,NF=8,ON=6,NC=4
在Rt△EFM中,![]()
∴![]()
在Rt△MFB中,![]()
在Rt△FNC中,![]()
又∵BC=10=100
∴BF+CF=BC
∴△BCF是直角三角形
即BF⊥CF
(3)由条件可知点G的纵坐标大于或等于-8小于或等于8.
①当点G的纵坐标为8时,如图,过点G作GK⊥x轴于K,交直线AB于R,
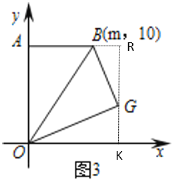
在Rt△OGK中,OG=OA=10,GK=8,可求OK=AR=6,RG=2,
∵BA=BG=m,BR=6-m,
在Rt△BRG中,由![]() ,
,
解得:m=![]() ;
;
②当点G的纵坐标为-8时,如图,过点G作GE⊥x轴于E,交直线AB于R,
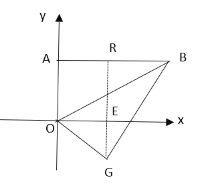
在Rt△OGE中,OG=OA=10,GE=8,
∴OE=AR=6,RE=OA=10,
∴GR=EG+RE=18,
∵∠BGR+∠OGE=∠OGE+∠EOG=90°,
∴∠BGR=∠EOG,
∵∠BRG=∠OEG=90°,
∴△BRG∽△EOG,
∴![]() ,即
,即![]() ,
,
解得:BR=24,
∴BA=m=AR+BR=6+24=30,
综上所述:当![]() ≤m≤30时,点G到x轴的距离不大于8.
≤m≤30时,点G到x轴的距离不大于8.
故答案为:![]() ≤m≤30.
≤m≤30.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:
(1)商场日销售量增加______件,每件商品盈利______.元(用含![]() 的代数式表示);
的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到1428元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() -1来表示
-1来表示![]() 的小数部分,事实上,小明的表示方法是有道理的,因为
的小数部分,事实上,小明的表示方法是有道理的,因为![]() <
<![]() <
<![]() ,所以
,所以![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.请据此解答:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.请据此解答:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)若设2+![]() 的整数部分为x,小数部分为y,求(y-x)2的值.
的整数部分为x,小数部分为y,求(y-x)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y![]() xb与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
xb与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
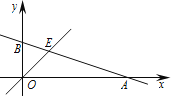
(1)求点A的坐标.
(2)在x轴上有一点P(m,0),过点P作x轴的垂线,与直线y![]() xb交于点C,与直线y=x交于点D.若CD≥5,求m的取值范围.
xb交于点C,与直线y=x交于点D.若CD≥5,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A、B两点,点A坐标为
的图象交于A、B两点,点A坐标为![]() ,点B坐标为
,点B坐标为![]() ,OA与x轴正半轴夹角的正切值为
,OA与x轴正半轴夹角的正切值为![]() ,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
(1)求一次函数与反比例函数的解析式;
(2)连接BD,求出BDC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
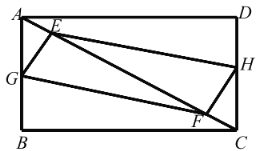
【题目】在矩形 ABCD 中,AB=3,BC=4,E、F 是对角线 AC 上的两个动点,分 别从 A、C 同时出发相向而行,速度均为每秒 1 个单位长度,运动时间为 t 秒,其中 0 t 5 .
(1)若 G,H 分别是 AB,DC 中点,求证:四边形 EGFH 是平行四边形(E、F 相遇时除外);
(2)在(1)条件下,若四边形 EGFH 为矩形,求 t 的值;
(3)若 G,H 分别是折线 A-B-C,C-D-A 上的动点,与 E,F 相同的速度同时出发,若 四边形 EGFH 为菱形,求 t 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com