
 已知Rt△ABC中,∠BAC=90°,M为AC的中点,N为BM中点,AN延长线交BC于P,过P作PQ∥AB交BM于Q.求证:
已知Rt△ABC中,∠BAC=90°,M为AC的中点,N为BM中点,AN延长线交BC于P,过P作PQ∥AB交BM于Q.求证:分析 (1)根据已知条件得到AN=NM,根据等腰三角形的判定得到∠AMB=∠MAN,通过全等三角形的性质得到AD=BM,推出四边形ABDM是矩形,由于PQ∥AB,得到四边形ABPQ是等腰梯形,得到∠QAN=∠PBN,根据外角的性质得到∠AQM=∠APC,根据相似三角形的判定定理即可得到结论;
(2)作ME∥BC交AP于E,由M为AC的中点,得到E我AP的中点,推出EM为△APC的中位线,得到EM=$\frac{1}{2}$PC,通过全等三角形的性质得到EM=BP,求得BP=$\frac{1}{2}$PC等量代换得到结论.
解答 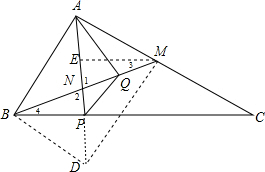 证明:(1)∵∠BAC=90°,N为BM的中点,
证明:(1)∵∠BAC=90°,N为BM的中点,
∴AN=NM,
∴∠AMB=∠MAN,
延长AP到D使ND=AN,连接MD,BD,
在△ABN与△DMN中,
$\left\{\begin{array}{l}{AN=DN}\\{∠ANB=∠MND}\\{BN=MN}\end{array}\right.$,
∴△ABN≌△MDN,
∴AD=BM,
∵∠BAC=90°,NA=NB=ND=NM,
∴四边形ABDM是矩形,
∵PQ∥AB,∴四边形ABPQ是等腰梯形,
∴∠QAN=∠PBN,∵∠AQM=∠QAN+∠1,∠APC=∠2+∠PBN,
∴∠AQM=∠APC,∵∠AMB=∠MAN,
∴△AQM∽△CPA;
(2)作ME∥BC交AP于E,
∵M为AC的中点,
∴E是AP的中点,
∴EM为△APC的中位线,
∴EM=$\frac{1}{2}$PC,
∵EM∥BC,
∴∠3=∠4,
在△EMN与△PBN中,
$\left\{\begin{array}{l}{∠3=∠4}\\{∠1=∠2}\\{BN=NM}\end{array}\right.$,
∴△EMN≌△PBN,
∴EM=BP,
∴BP=$\frac{1}{2}$PC,
∵∠BAC=90°,N是BM的中点,
∴AM=BN,
∴∠BAN=∠ABN,
∵PQ∥AB,
∴∠NPQ=∠NQP,
∴NQ=BP,
∴AQ=$\frac{1}{2}$PC.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,三角形的中位线的性质,平行线的性质,等腰梯形的判定和性质,正确的作出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
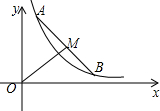 如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
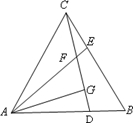 如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.
如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
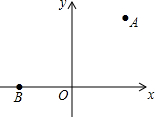 如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).
如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
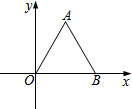 如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )| A. | (2,$\sqrt{3}$) | B. | (2,4) | C. | (2,2$\sqrt{3}$) | D. | (2$\sqrt{3}$,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
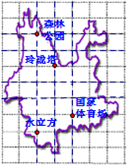 我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )| A. | (-2,-4) | B. | (-1,-4) | C. | (-2,4) | D. | (-4,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 34.383×1011 | B. | 3.4383×1012 | C. | 3.4383×1013 | D. | 3.4383×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com