
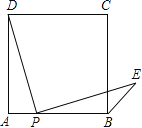
【题目】点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得到线段PE,连接BE,则∠CBE等于 .
【答案】45°
【解析】
试题在AD上取一点F,使DF=BP,连接PF,由正方形的性质就可以得出△DFP≌△PBE,就可以得出∠DFP=∠PBE,根据AP=AF就可以得出∠DFP的值,就可以求出∠CBE的值.
解:在AD上取一点F,使DF=BP,连接PF,
∵四边形ABCD是正方形,
∴AD=AB,∠A=∠ABC=90°.
∴AD﹣DF=AB﹣BP,∠ADP+∠APD=90°,
∴AF=AP.
∴∠AFP=∠APF=45°,
∴∠DFP=135°.
∵∠DPE=90°
∴∠APD+∠BPE=90°.
∴∠ADP=∠BPE.
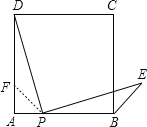
在△DFP和△PBE中,
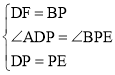 ,
,
∴△DFP≌△PBE(SAS),
∴∠DFP=∠PBE,
∴∠PBE=135°,
∴∠EBC=135°﹣90°=45°.
故答案为:45°.


科目:初中数学 来源: 题型:
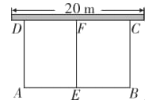
【题目】如图,某校“综合实践”社团,计划利用![]() 长的栅栏材料,一边靠原有旧墙围成如图所示的两个矩形试验田,墙的长度为
长的栅栏材料,一边靠原有旧墙围成如图所示的两个矩形试验田,墙的长度为![]() .
.
(1)能否围成总面积为![]() 的试验田?若能,求出
的试验田?若能,求出![]() 的长度;若不能,说明理由;
的长度;若不能,说明理由;
(2)能否围成总面积为![]() 的试验田?说说你的理由.
的试验田?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P到图形Ω(可以是线段、三角形、圆或不规则图形等)的距离是指:点P与图形Ω中所有点连接的线段中最短线段的长度.如图①中的两个虚线段PQ的长度都表示点P到图形Ω的距离.

如图②,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为![]() ,点P从原点出发,以每秒1个单位长度的速度向x轴的正方向运动了t秒.
,点P从原点出发,以每秒1个单位长度的速度向x轴的正方向运动了t秒.

(1)当t=0时,求点P到△ABC的距离;
(2)当点P到△ABC的距离等于线段AP的长度时,求t的范围;
(3)当点P到△ABC的距离大于![]() 时,求t的取值范围.
时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球和足球.已知购买20个篮球和40个足球的总金额为4600元;购买30个篮球和50个足球的总金额为6100元.
(1)每个篮球、每个足球的价格分别为多少元?
(2)若该校购买篮球和足球共60个,且购买篮球的总金额不超过购买足球的总金额,则该校最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个自然数从高位到个位是由一个数字或几个数字重复出现组成的,那么我们把这样的自然数叫做循环数,重复的一个或几个数字称为“循环节”,我们把“循环节”的数字个数叫做循环节的阶数.例如:525252,它由“52”依次重复出现组成,所以525252是循环数,它是2阶6位循环数.再如:77,是1阶2位循环数,135135135是3阶9位循环数.
(1)请直接写出1个2阶4位循环数 ,并证明对于任意一个2阶4位循环数,若交换其循环节的数字得到一个新的4位数,则该新数和原数的差能够被9整除.
(2)已知一个能被9整除的2阶4位数.设循环节为ab,且满足a﹣2b为非负偶数,求这个4位循环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点.
(1)求m的取值范围;
(2)当m取满足条件的最大整数时,求抛物线与x轴有两个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
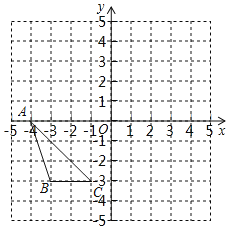
【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个顶点的坐标分别为A(﹣4,0),B(﹣3,﹣3),C(﹣1,﹣3).
(1)画出△ABC关于x轴对称的△ADE(其中点B,C的对称点分别为点D、E);
(2)画出△ABC关于原点成中心对称的△FGH(其中A、B、C的对称点分别为点F,G,H).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com