
�졢�������ֱ�����480ǧ��·�̵ļס�������ͬʱ������������ʻ����������У�;���������ͣ��1Сʱ��Ȼ����ԭ�ټ��������ʻ������غ�ֹͣ��ʻ���쳵�����ҵغ�������ԭ·ԭ�ٷ��ؼأ��쳵��ͷ��ʱ����Բ��ƣ����졢���������ҵص�·��y��ǧ�ף�������ʱ��x��Сʱ��֮��ĺ���ͼ����ͼ������ͼ����Ϣ����������⣺

��1��ֱ��д����������ʻ�ٶȺ�a��ֵ��
��2���쳵��������һ������ʱ������ص�·���Ƕ���ǧ�ף�
��3������������Сʱ����·��Ϊ200ǧ�ף���ֱ��д���𰸣�
�⣺��1�������⣬��
�������ٶ�Ϊ��480�£�9��1��=60ǧ��/ʱ��
��a=60����7��1��=360��
����������ʻ�ٶ�Ϊ60ǧ��/ʱ��a=360ǧ�ף�
��2�������⣬��
5��60=300��
��D��5��300������yOD=k1x�������⣬��
300=5k1��
��k1=60��
��yOD=60x��
�߿쳵���ٶ�Ϊ����480+360����7=120ǧ��/ʱ��
��480��120=4Сʱ��
��B��4��0����C��8��480����
��yAB=k2x+b�������⣬��
 ��
��
��ã�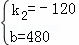 ��
��
��yAB=��120x+480
��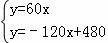 ��
��
��ã�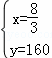 ��
��
��480��160=320ǧ�ף�
�𣺿쳵��������һ������ʱ������ص�·����320ǧ�ף�
��3����ֱ��BC�Ľ���ʽΪyBC=k3x+b3�������⣬��
 ��
��
��ã�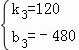 ��
��
��yBC=120x��480��
��ֱ��EF�Ľ���ʽΪyEF=k4x+b4�������⣬��
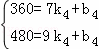 ��
��
��ã�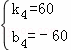 ��
��
��yEF=60x��60��
��60x������120x+480��=200ʱ��
��ã�x=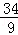 ��
��
��60x������120x+480��=��200ʱ
��ã�x=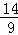 ��
��
��120x��480����60x��60��=200ʱ��
��ã�x=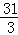 ��9����ȥ����
��9����ȥ����
��120x��480����60x��60��=��200ʱ
��ã�x=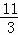 ��4����ȥ����
��4����ȥ����
��120x��480��60x=��200ʱ
��ã�x=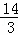 ��
��
������������������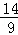 Сʱ��
Сʱ��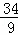 Сʱ��
Сʱ��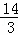 Сʱʱ����������·��Ϊ200ǧ�ף�
Сʱʱ����������·��Ϊ200ǧ�ף�


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
���� ��
��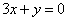 ��
��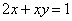 ��
��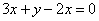 ��
��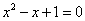 �У���Ԫһ�η��̵ĸ����ǣ�������
�У���Ԫһ�η��̵ĸ����ǣ�������
A.1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ȫ�����ض�����������ũ��ҽ�ƺ����ƶȣ�����ֻҪÿ��ÿ�꽻50ԪǮ���Ϳ��Լ������ҽ�ƣ�ÿ�������Լ�֧��ҽ�Ʒѣ�����ʱ�ɵõ���һ���������صķ��ؿС����ͬѧ����������������һЩũ�����ռ��������ݻ��������µ�ͳ��ͼ��
�����������Ϣ������⣺
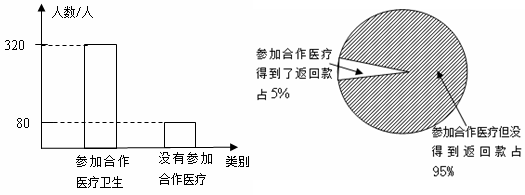
��1�����ε����˶��ٴ�������Ĵ����У��ж����˲μӺ���ҽ�Ƶõ��˷��ؿ
��2����������10000��������������ж����˲μ��˺���ҽ�ƣ�Ҫʹ�����μӺ���ҽ�Ƶ��������ӵ�9680�ˣ����������������������ͬ��������������ʣ�
������2013����ͷ婽���ģ����ıࣩ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ������2��3��x��y��12�У�Ψһ��������12��ƽ������6���������ݵ���λ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ABCD�У�AB=2��BC=1����P��ֱ��BD��һ�㣬��DP=DA��ֱ��AP��ֱ��BC���ڵ�E����CE=��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���м�����ȷ���ǣ�������
| �� | A�� | a3+a4=a7 | B�� | a3•a4=a7 | C�� | a6•a3=a2 | D�� | ��a3��4=a7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
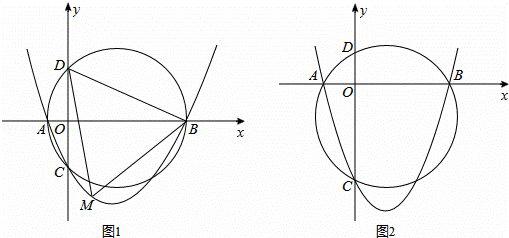
ͼ����֪������y=ax2+bx+c��a��0��c��0����x���ڵ�A��B����y���ڵ�C�������A��B��C�����Բ��y�����һ������ΪD��
��1����ͼ1����֪��A��B��C������ֱ�Ϊ����2��0������8��0������0����4����
����������ߵı���ʽ���D�����ꣻ
������MΪ�������ϵ�һ���㣬��λ�ڵ������ޣ����BDM��������ֵ��
��2����ͼ2����a=1����֤������b��cȡ��ֵ����D��Ϊ���㣬����ö������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Լ������һ��������(��Ϊ��A1)������һ��������(��Ϊ��A)ͨ��һ��ƽ�ƣ���������һ�ߵ��е���ת180��õ��ģ���ơ�A1���ɡ�A���Ƶģ����µIJ�����ÿһ��������ֻ���Ը���һ�Σ����ƹ��̿���һֱ������ȥ����ͼ1���ɡ�A���Ƴ���A1�����ɡ�A1���Ƴ���A2�����ɡ�A2���Ƴ���A3���γ���һ���������Σ�������B.���¸����еĸ��ƾ����ɡ�A��ʼ�ģ�ͨ�������γɵĶ�����е�������������С������(ָ���Aȫ�ȵ�������)֮�����϶Ҳ���ص���
(1)ͼ1�б������һ�ֿ��ܵĸ��ƽ����С�����֡�A�ס�B�������Ʊ�Ϊ__________����ͼ1�Ļ����ϼ���������ȥ�õ���C������C��һ������ǡ ��11��С������(ָ��һ�����ڸñ��ϵ�С������)�����C�к���__________��С�����Σ�
��11��С������(ָ��һ�����ڸñ��ϵ�С������)�����C�к���__________��С�����Σ�
(2)����A���������Σ�����Ϊͨ���������γɵ����������__________��
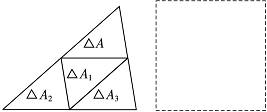 (3)������������ת��һ��ƽ�Ƹ����γ�һ���ı��Σ���ͼ2�ķ����ڻ�����ͼ��������ͼ1������ǣ�
(3)������������ת��һ��ƽ�Ƹ����γ�һ���ı��Σ���ͼ2�ķ����ڻ�����ͼ��������ͼ1������ǣ�
ͼ1 ͼ2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com