
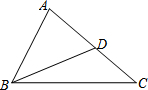
 如图,△ABC中,D是边AC上一点,连接BD.要使△ABD∽△ACB,需要补充的一个条件为∠ABD=∠C或∠ADB=∠ABC或AB2=AD•AC.
如图,△ABC中,D是边AC上一点,连接BD.要使△ABD∽△ACB,需要补充的一个条件为∠ABD=∠C或∠ADB=∠ABC或AB2=AD•AC.  课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y=k1x+b与双曲线$y=\frac{k_2}{x}$相交于点A(2,4),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,求直线和双曲线的解析式.
已知直线y=k1x+b与双曲线$y=\frac{k_2}{x}$相交于点A(2,4),且与x轴、y轴分别交于B、C两点,AD垂直平分OB,垂足为D,求直线和双曲线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
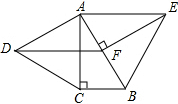 如图,分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE,已知∠BAC=30°,BC=1,EF⊥AB,垂足为F,连结DF.
如图,分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE,已知∠BAC=30°,BC=1,EF⊥AB,垂足为F,连结DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )
如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )| A. | 9:4 | B. | 3:2 | C. | $\sqrt{3}:\sqrt{2}$ | D. | $3\sqrt{3}:2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com