
����Ŀ��ijУ���꼶����800��ѧ�������������Ƕ�����̼��֪ʶ���˽�̶ȣ�
��1����ȷ�����鷽ʽʱ����ί������������ַ�����
����һ��������꼶����Ů����
��������������꼶����������
�������������꼶ÿ����ȥ�������һ��������ѧ����
������������д����Ե�һ��������_____��
��2����ί����������д����Եĵ��鷽���������ռ��������ݻ��Ƴ�������������ͳ��ͼ����ͼ����ͼ����ʾ�����������ͼ����Ϣ��������ͳ��ͼ����������
��3��������Ƹ�У���꼶Լ�ж�����ѧ���Ƚ��˽�����̼��֪ʶ��
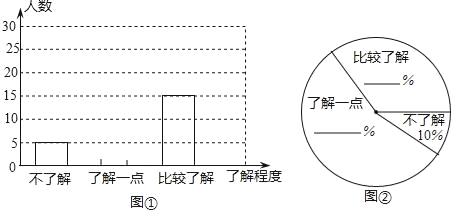
���𰸡���1������������2������������3��240
�������������������1������ѧ�������Ƚ϶࣬���ó������鷽ʽ������һ��������ֻ�漰��������Ů��һ�����棬����Ƭ�棬��Ӧѡ��������
��2�����ݲ��˽�Ϊ5�ˣ���ռ�ٷֱ�Ϊ10%���ó��������������������������ȥ���˽�ͱȽ��˽�������ó��˽�һ�����������ռ�İٷֱȣ���������1��ȥ�˽�һ��ĺͲ��˽����ռ�İٷֱ�����Ƚ��˽���ռ�İٷֱȣ��Ӷ���ȫͳ��ͼ��
��3�������������ԡ��Ƚ��˽⡱��ռ�ٷֱȼ�����⣮
�����������1������һ��������ֻ�漰��������Ů��һ�����棬����Ƭ�棬��Ӧѡ��������
��2����������ã�
![]() =50���ˣ���
=50���ˣ���
�˽�һ��������ǣ�50��5��15=30���ˣ���
�˽�һ���������ռ�İٷֱ��ǣ�![]() ��100%=60%��
��100%=60%��
�Ƚ��˽����ռ�İٷ��ǣ�1��60%��10%=30%��
��ͼ���£�
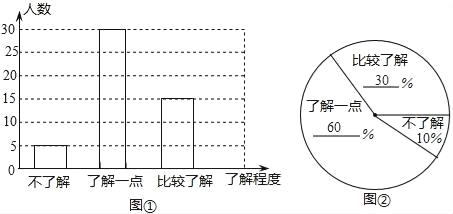
��3����������ã�800��30%=240��������
�𣺸�У���꼶Լ��240��ѧ���Ƚ��˽�����̼��֪ʶ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ȫ��ͬ��������ֽƬABC��DEC�غϷ��ã�����![]() ��
��![]() .
.
��1����������
�ٹ̶�![]() ��ʹ
��ʹ![]() �Ƶ�C��ת.����Dǡ������AB����ʱ����ͼ2�����߶�DE��AC��λ�ù�ϵ��________����֤����
�Ƶ�C��ת.����Dǡ������AB����ʱ����ͼ2�����߶�DE��AC��λ�ù�ϵ��________����֤����
����![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ��������ϵ��________.
��������ϵ��________.
��2��������֤
��![]() �Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����
�Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����![]() ��
��![]() ��������ϵ��Ȼ����������ֱ�����
��������ϵ��Ȼ����������ֱ�����![]() ��
��![]() ��BC��CE���ϵĸߣ����ɴ�֤��С���IJ���.
��BC��CE���ϵĸߣ����ɴ�֤��С���IJ���.
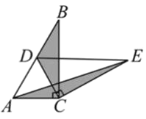
��3����չ̽��
��֪![]() ����D�����ƽ������һ�㣬
����D�����ƽ������һ�㣬![]() ��
��![]() ��BC�ڵ�E����ͼ4��������������BA���Ƿ���ڵ�F��ʹ
��BC�ڵ�E����ͼ4��������������BA���Ƿ���ڵ�F��ʹ![]() �������ڣ���ֱ��д�����������ĵ�F�ĸ������������ڣ���˵������.
�������ڣ���ֱ��д�����������ĵ�F�ĸ������������ڣ���˵������.
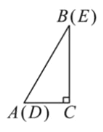
ͼ1 ͼ2
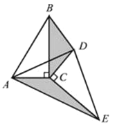
ͼ3 ͼ4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
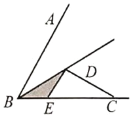
����Ŀ����֪����ͼ��E��F ��ƽ���ı��� ABCD �ĶԽ��� AC �ϵ����㣬AE=CF��

��֤����1��EB DF ��
��2��EB��DF ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�![]() ����C��
����C��![]() ����B��
����B��
��1��������ABC�����![]() _____________��
_____________��
��2����ͼ2����B��![]() ��y����D����AE��DE�ֱ�ƽ�֡�CAB����ODB�����AED�Ķ�����
��y����D����AE��DE�ֱ�ƽ�֡�CAB����ODB�����AED�Ķ�����
��3����P��y���ϣ�ʹ��������ABC��������ACP�������ȣ�ֱ��д��P�����꣮



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ԥ��������ij��λ�칫�Ҳ���ҩѬ������������������֪ҩ��ȼ��ʱ������ÿ���������еĺ�ҩ��y(����)��ʱ��x(����)��Ϊ��������ҩ��ȼ�պ�y��x�ɷ�����(��ͼ)���ֲ��ҩ��8����ȼ�ϣ���ʱ���ڿ�����ÿ�����ĺ�ҩ��6���ˣ�������������ṩ����Ϣ������������⣺

(1)ҩ��ȼ��ʱ��y����x�ĺ�����ϵʽΪ________���Ա���x��ȡֵ��Ϊ________��ҩ��ȼ�պ�y����x�ĺ�����ϵʽΪ________��
(2)�о���������������ÿ�����ĺ�ҩ������1.6����ʱԱ�����ɽ��칫�ң���ô��������ʼ��������Ҫ����________���Ӻ�Ա�����ܻص��칫�ң�
(3)�о���������������ÿ�����ĺ�ҩ��������3�����ҳ���ʱ�䲻����10����ʱ��������Чɱ������еIJ�������ô�˴������Ƿ���Ч��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
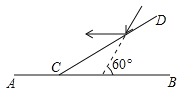
����Ŀ����֪��ͼ��һ��������ˮƽ���60��ĽǶ�������棬���ڵ���AB��֧��һ��ƽ�澵CD��ʹ��������ƽ�澵�����ˮƽ���ߣ���ƽ�澵CD�����AB���ɽǡ�DCB�Ķ�������______��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD����ͼ�٣������²����������1���Թ���A��ֱ��Ϊ�ۺ��۵�ֽƬ��ʹ��Bǡ������AD���ϣ��ۺ���BC�߽��ڵ�E����ͼ�ڣ�����2���Թ���E��ֱ��Ϊ�ۺ��۵�ֽƬ��ʹ��A����BC���ϣ��ۺ�EF��AD���ڵ�F����ͼ�ۣ�����3����ֽƬչƽ����ô��AFE�Ķ���Ϊ_________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij�칫��¥��ǰ����һ���߶���15�����ED���Ӱ칫��¥����A�����˶���E�ĸ��Ǧ���45�㣬��˵Ͷ�D����¥ǰ�ݿ��ױߵľ���DC��20�ף��ݿ��³�BC��12�ף��ݿ��¶�i=1:![]() �����¥AB�ĸ߶�Ϊ_________�ף�
�����¥AB�ĸ߶�Ϊ_________�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
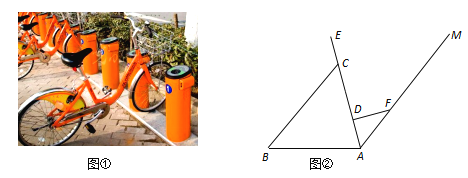
����Ŀ������̼����������ͬ�С��������꣬������еĹ������г���������д����˼���ķ��㣮ͼ���ǹ������г���ʵ��ͼ��ͼ���ǹ������г��ij���ʾ��ͼ����A��D��C��E��ͬһ��ֱ���ϣ�CD=30cm��DF=20cm��AF=25cm��FD��AE�ڵ�D������CE=15cm���ҡ�EAB=75�㣮
��1����AD�ij���
��2�����E��AB�ľ��룮���ο����ݣ�sin75���0.97��cos75���0.26��tan75���3.73��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com