
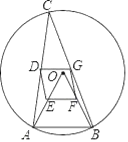
【题目】如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.
(1)试判断四边形DEFG的形状,并说明理由;
(2)填空:
①若AB=3,当CA=CB时,四边形DEFG的面积是 ;
②若AB=2,当∠CAB的度数为 时,四边形DEFG是正方形.
【答案】(1)详见解析;(2)①![]() ;②75°或15°.
;②75°或15°.
【解析】
(1)只要证明DG=EF,DG∥EF即可解决问题;
(2)①只要证明四边形DEFG是矩形即可解决问题;
②分点C在优弧AB或劣弧AB上两种情况讨论即可.
解:(1)四边形DEFG是平行四边形.
∵点D、E、F、G分别是CA、OA、OB、CB的中点,
∴DG∥AB,DG=![]() AB,EF∥AB,EF=
AB,EF∥AB,EF=![]() AB,
AB,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)①连接OC,

∵CA=CB,
∴![]() ,
,
∴DG⊥OC,
∵AD=DC,AE=EO,
∴DE∥OC,DE=![]() OC=1,同理EF=
OC=1,同理EF=![]() AB=
AB=![]() ,
,
∴DE⊥DG,
∴四边形DEFG是矩形,
∴四边形DEFG的面积=![]() .
.
故答案为![]() ;
;
②∵OA=OB=AB=2,
∴△AOB为等边三角形,
由①可得:当C是优弧AB的中点时,四边形DEFG是正方形,此时∠C=![]() ∠AOB=30°,则∠CAB=75°;
∠AOB=30°,则∠CAB=75°;
当C是劣弧AB的中点时,四边形DEFG是正方形,此时∠C=![]() (360°﹣∠AOB)=150°,则∠CAB=15°;
(360°﹣∠AOB)=150°,则∠CAB=15°;
故答案为75°或15°.


科目:初中数学 来源: 题型:
【题目】码头工人每天往一艘轮船50吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)若原有码头工人10名,在(2)的条件下,至少需要增加多少名工人才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
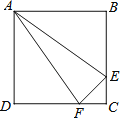
A. 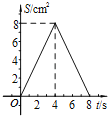 B.
B. 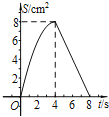
C. 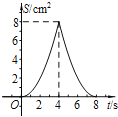 D.
D. 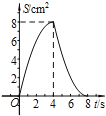
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )
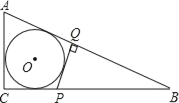
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为_____.
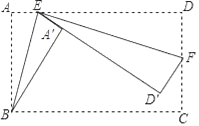
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置.设BC=2,AC=2![]() ,则顶点A运动到点A″的位置时,点A经过的路线与直线l所围成的面积是_____.
,则顶点A运动到点A″的位置时,点A经过的路线与直线l所围成的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
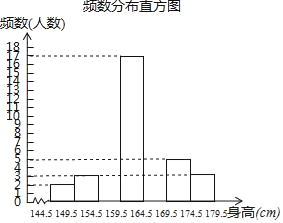
【题目】为了解同学们的身体发育情况,学校体卫办公室对七年级全体学生进行了身高测量(精确到1cm),并从中抽取了部分数据进行统计,请根据尚未完成的频数分布表和频数分布直方图解答下列问题:
频率分布表
分组 | 频数 | 百分比 |
144.5~149.5 | 2 | 4% |
149.5~154.5 | 3 | 6% |
154.5~159.5 | a | 16% |
159.5~164.5 | 17 | 34% |
164.5~169.5 | b | n% |
169.5~174.5 | 5 | 10% |
174.5~179.5 | 3 | 6% |
(1)求a、b、n的值;
(2)补全频数分布直方图;
(3)学校准备从七年级学生中选拔护旗手,要求身高不低于170cm,如果七年级有学生350人,护旗手的候选人大概有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com