
【题目】我们来定义一种新运算:对于任意实数x、y,“※”为a※b=(a+1)(b+1)﹣1
(1)计算(﹣3)※9
(2)嘉琪研究运算“※”之后认为它满足交换律,你认为她的判断 (正确、错误)
(3)请你帮助嘉琪完成她对运算“※”是否满足结合律的证明.
证明:由已知把原式化简得a※b=(a+1)(b+1)﹣1=ab+a+b
∵(a※b)※c=(ab+a+b)※c=
a※(b※c)=
∴
∴运算“※”满足结合律.

【答案】(1)﹣21(2)正确;(3)abc+ac+ab+bc+a+b+c;abc+ac+ab+bc+a+b+c;(a※b)※c=a※(b※c)
【解析】
(1)根据新定义运算法则即可求出答案.
(2)只需根据整式的运算证明法则a※b=b※a即可判断.
(3)只需根据整式的运算法则证明(a※b)※c=a※(b※c)即可判断.
(1)(﹣3)※9=(﹣3+1)(9+1)﹣1=﹣21
(2)a※b=(a+1)(b+1)﹣1
b※a=(b+1)(a+1)﹣1,
∴a※b=b※a,
故满足交换律,故她判断正确;
(3)由已知把原式化简得a※b=(a+1)(b+1)﹣1=ab+a+b
∵(a※b)※c=(ab+a+b)※c
=(ab+a+b+1)(c+1)﹣1
=abc+ac+ab+bc+a+b+c
∵a※(b※c)=a(bcv+b+c)+(bc+b+c)+a=abc+ac+ab+bc+a+b+c
∴(a※b)※c=a※(b※c)
∴运算“※”满足结合律
故答案为:(2)正确;(3)abc+ac+ab+bc+a+b+c;abc+ac+ab+bc+a+b+c;(a※b)※c=a※(b※c)


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
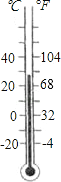
【题目】温度与我们的生活息息相关,你仔细观察过温度计吗?如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉),设摄氏温度为x(℃),华氏温度为y(℉),则y是x的一次函数.
(1)仔细观察图中数据,试求出y与x之间的函数表达式;
(2)当摄氏温度为零下15℃时,求华氏温度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a∥b,a,b之间的距离为4,点P到直线a的距离为4,点Q到直线b的距离为2,PQ=2![]() .在直线a上有一动点A,直线b上有一动点B,满足AB⊥b,且PA+AB+BQ最小,此时PA+BQ=________.
.在直线a上有一动点A,直线b上有一动点B,满足AB⊥b,且PA+AB+BQ最小,此时PA+BQ=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术饰品 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com