考点:四点共圆,平行线的性质,垂径定理,圆周角定理,切线长定理
专题:证明题
分析:(1)连接OA、OB、OP,根据切线的性质、切线长定理及平行线的性质可证到∠PDB=∠POB,从而可得P、B、D、O四点共圆,由∠PAO+∠PBO=180°可得P、B、O、A四点共圆,就可得到D、A、O、P、B共圆.
(2)由P、B、D、O四点共圆可得∠ODP=∠OBP=90°,即OD⊥MN,根据垂径定理就可得到D为弦MN中点.
解答:证明:(1)

连接OA、OB、OP,如图所示.
∵PA、PB是圆的切线,
∴PA=PB,OA⊥PA,OB⊥PB,∠APO=∠BPO,
∴∠AOP=∠POB.
∵∠C=
∠AOB,
∴∠C=∠POB
∵PD∥AC,
∴∠C=∠PDB,
∴∠PDB=∠POB,
∴P、B、D、O四点共圆.
∵∠PAO+∠PBO=180°,
∴P、B、O、A四点共圆,
∴D、A、O、P、B共圆.
(2)∵P、B、D、O四点共圆,
∴∠ODP=∠OBP=90°,
∴OD⊥MN,
∴DN=DM,即D为弦MN中点.
点评:本题主要考查了四点共圆的判定、切线长定理、圆周角定理、垂径定理、平行线的性质等知识,掌握四点共圆的判定方法(判定1:若线段同侧的两点对线段的张角相等,则这两点以及线段的两个端点共圆;判定2:若四个点构成的四边形的对角互补或外角等于内对角,则这四点共圆)是解决本题的关键.

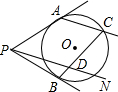 如图,PA与PB切⊙O于A、B,C为优弧
如图,PA与PB切⊙O于A、B,C为优弧
 连接OA、OB、OP,如图所示.
连接OA、OB、OP,如图所示.

 名师点拨卷系列答案
名师点拨卷系列答案
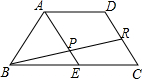 在等腰梯形ABCD中,下底BC是上底AD的两倍,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=( )
在等腰梯形ABCD中,下底BC是上底AD的两倍,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=( )