
| 类型 价格 | 进价(元/盏) | 售价(元/盏) |
| A型 | 30 | 45 |
| B型 | 50 | 70 |


科目:初中数学 来源:不详 题型:解答题
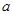 ,
,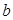 是任意两个不等实数,我们规定:满足不等式
是任意两个不等实数,我们规定:满足不等式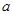 ≤
≤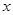 ≤
≤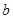 的实数
的实数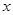 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为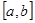 . 对于一个函数,如果它的自变量
. 对于一个函数,如果它的自变量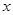 与函数值
与函数值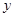 满足:当m≤
满足:当m≤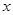 ≤n时,有m≤
≤n时,有m≤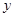 ≤n,我们就称此函数是闭区间
≤n,我们就称此函数是闭区间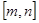 上的“闭函数”.
上的“闭函数”.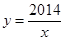 是闭区间
是闭区间 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由; 是闭区间
是闭区间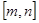 上的“闭函数”,求此函数的表达式;
上的“闭函数”,求此函数的表达式;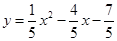 是闭区间
是闭区间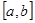 上的“闭函数”,直接写出实数
上的“闭函数”,直接写出实数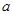 ,
,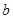 的值.
的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=2x | B.y=?2x | C.y= x x | D.y=? x x |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.直线x=1 | B.直线x=-2 |
| C.直线x=-1 | D.直线x=-4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象如图所示,下列结论正确的是
的图象如图所示,下列结论正确的是| A.它们的函数值y随着x的增大而增大 |
| B.它们的函数值y随着x的增大而减小 |
| C.k<0 |
| D.它们的自变量x的取值为全体实数 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com