
 )2+25,解此方程即可求得答案;
)2+25,解此方程即可求得答案; 的取值范围,则可求得R的取值范围,继而求得答案.
的取值范围,则可求得R的取值范围,继而求得答案. =
=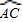 ,
,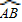 =
=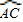 ,
, BC=
BC= ×10=5(cm),
×10=5(cm),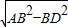 =
=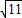 (cm),
(cm),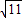 )cm,
)cm,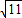 )2+25,
)2+25,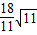 (cm);
(cm);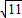 <4,
<4,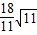 <6
<6

科目:初中数学 来源: 题型:
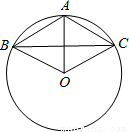
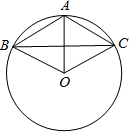 如图,已知⊙O上的三点A、B、C,且AB=AC=6cm,BC=10cm
如图,已知⊙O上的三点A、B、C,且AB=AC=6cm,BC=10cm查看答案和解析>>
科目:初中数学 来源:2013届江苏泰州中学附属初中九年级第一次考试数学试卷(带解析) 题型:解答题
如图,已知⊙O上的三点A、B、C,且AB="AC=6" cm,BC=10cm
(1)求证:∠AOB=∠AOC
(2)求圆片的半径R(结果保留根号);
(3)若在(2)题中的R的值满足n<R<m(其中m、n为正整数),试估算m的最小值和n的最大值.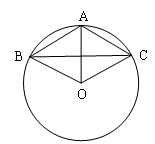
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏泰州中学附属初中九年级第一次考试数学试卷(解析版) 题型:解答题
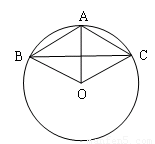
如图,已知⊙O上的三点A、B、C,且AB=AC=6 cm,BC=10cm
(1)求证:∠AOB=∠AOC
(2)求圆片的半径R(结果保留根号);
(3)若在(2)题中的R的值满足n<R<m(其中m、n为正整数),试估算m的最小值和n的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
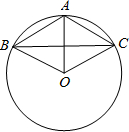 如图,已知⊙O上的三点A、B、C,且AB=AC=6cm,BC=10cm
如图,已知⊙O上的三点A、B、C,且AB=AC=6cm,BC=10cm查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com