
【题目】如图,y关于x的二次函数y=﹣![]() (x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
(x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
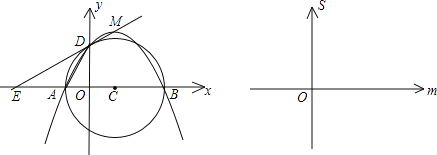
(1)写出A、B、D三点的坐标;
(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;
(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
【答案】(1)A(﹣m,0),B(3m,0),D(0,![]() m).(2)直线ED与⊙C相切.(3)见解析
m).(2)直线ED与⊙C相切.(3)见解析
【解析】
试题分析:(1)根据x轴,y轴上点的坐标特征代入即可求出A、B、D三点的坐标;
(2)待定系数法先求出直线ED的解析式,再根据切线的判定得出直线与圆的位置关系;
(3)分当0<m<3时,当m>3时两种情况讨论求得关于m的函数.
解:(1)令y=0,则﹣![]() (x+m)(x﹣3m)=0,解得x1=﹣m,x2=3m;
(x+m)(x﹣3m)=0,解得x1=﹣m,x2=3m;
令x=0,则y=﹣![]() (0+m)(0﹣3m)=
(0+m)(0﹣3m)=![]() m.
m.
故A(﹣m,0),B(3m,0),D(0,![]() m).
m).
(2)设直线ED的解析式为y=kx+b,将E(﹣3,0),D(0,![]() m)代入得:
m)代入得:
![]()
解得,k=![]() ,b=
,b=![]() m.
m.
∴直线ED的解析式为y=![]() mx+
mx+![]() m.
m.
将y=﹣![]() (x+m)(x﹣3m)化为顶点式:y=﹣
(x+m)(x﹣3m)化为顶点式:y=﹣![]() (x﹣m)2+
(x﹣m)2+![]() m.
m.
∴顶点M的坐标为(m,![]() m).代入y=
m).代入y=![]() mx+
mx+![]() m得:m2=m
m得:m2=m
∵m>0,
∴m=1.所以,当m=1时,M点在直线DE上.
连接CD,C为AB中点,C点坐标为C(m,0).
∵OD=![]() ,OC=1,
,OC=1,
∴CD=2,D点在圆上
又∵OE=3,DE2=OD2+OE2=12,
EC2=16,CD2=4,
∴CD2+DE2=EC2.
∴∠EDC=90°
∴直线ED与⊙C相切.
(3)当0<m<3时,S△AED=![]() AE.OD=
AE.OD=![]() m(3﹣m)
m(3﹣m)
S=﹣![]() m2+
m2+![]() m.
m.
当m>3时,S△AED=![]() AEOD=
AEOD=![]() m(m﹣3).
m(m﹣3).
即S=![]() m2_
m2_ ![]() m.
m.
S关于m的函数图象的示意图如右:



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,三角形ABC的三个顶点和点P都在小方格的顶点上.

(1)请在图1中,画出将三角形ABC绕点C旋转后的三角形A1B1C,使得点P落在三角形A1B1C内部,且三角形A1B1C的顶点也都落在方格的顶点上.
(2)写出旋转角的度数 .
(3)拓展延伸:如图2,将直角三角形ABC(其中∠C=90°)绕点A按顺时针方向选择115°得到△AB1C1,使得点C,A,B1在同一条直线上,那么∠BAC1等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F分别是平行四边形ABCD的边AB,DC上的点,AF与DE相交于点P,FB与EC相交于点B,若S△APD=15cm2,S△BQC=25cm2,则阴影部分的面积为( )
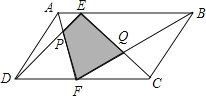
A.10cm2 B.20cm2 C.30cm2 D.40cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
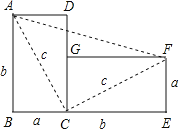
【题目】如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在红城中学举行的“我爱祖国”征文活动中,七年级和八年级共收到征文118篇,且七年级收到的征文篇数是八年级收到的征文篇数的一半还少2篇,求七年级收到的征文有多少篇?
查看答案和解析>>
科目:初中数学 来源: 题型:
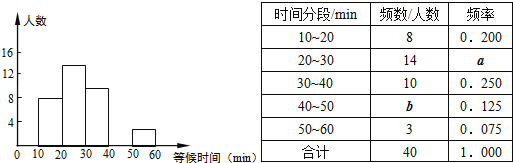
【题目】某公园元旦期间,前往参观的人非常多.这期间某一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)表中a= ,b= ,并请补全频数分布直方图;
(3)在调查人数里,若将时间分段内的人数绘成扇形统计图,则“40~50”的圆心角的度数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com