
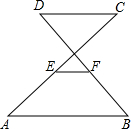
 如图,AB∥CD,E、F分别为AC、BD的中点,若AB=7,CD=4,则EF的长是$\frac{3}{2}$.
如图,AB∥CD,E、F分别为AC、BD的中点,若AB=7,CD=4,则EF的长是$\frac{3}{2}$. 分析 首先连接CF,并延长交AB于点G,易证得△CDF≌△GBF(ASA),即可求得CF=GF,CD=GB=4,继而可得EF是△ACG的中位线,则可求得答案.
解答  解:连接CF,并延长交AB于点G,
解:连接CF,并延长交AB于点G,
∵AB∥CD,
∴∠CDF=∠GBF,
在△CDF和△GBF中,
$\left\{\begin{array}{l}{∠CDF=∠GBF}\\{DF=BF}\\{∠DFC=∠BFG}\end{array}\right.$,
∴△CDF≌△GBF(ASA),
∴CF=GF,CD=GB=4,
∴AG=AB-BG=7-4=3,
又∵E为AC的中点,
∴EF是△ACG的中位线,
∴EF=$\frac{1}{2}$AG=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 此题考查了梯形的性质、全等三角形的判定与性质以及三角形的中位线的性质.注意掌握辅助线的作法,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
| 数量x(千克) | 1 | 2 | 3 | 4 | 5 |
| 售价y(元) | 3+0.1 | 6+0.2 | 9+0.3 | 12+0.4 | 15+0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 张师傅要在如图所示的钝角三角形铁片上截取一个面积最大的半圆形工件,如果要求半圆形工件的直径恰好在三角形铁片的最长边上.
张师傅要在如图所示的钝角三角形铁片上截取一个面积最大的半圆形工件,如果要求半圆形工件的直径恰好在三角形铁片的最长边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
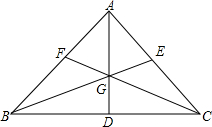 如图在△ABC中,点D、E、F分别在三边上,E是AC中点.AD、BE、CF交于点G,BD=2DC,S△GCE=4,S△GCD=5,求△ABC的面积?
如图在△ABC中,点D、E、F分别在三边上,E是AC中点.AD、BE、CF交于点G,BD=2DC,S△GCE=4,S△GCD=5,求△ABC的面积?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com