
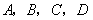 在
在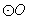 上,
上,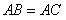 ,
,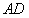 与
与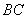 相交于点E,
相交于点E,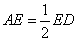 ,延长
,延长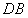 到点
到点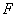 ,使
,使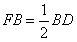 ,连结
,连结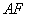 .求证:直线
.求证:直线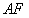 与
与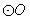 相切
相切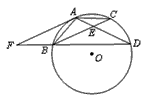
 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
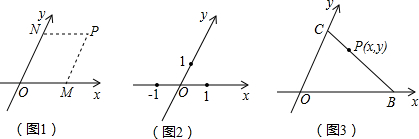
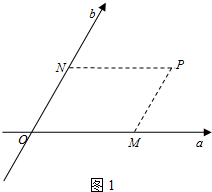 如图1,在平面内取一点O,过点O作两条夹角为60°的数轴,使它们以点O为公共原点且具有相同的单位长度,这样在平面内建立的坐标系称为斜坐标系,我们把水平放置的数轴称为横轴(记作a轴),将斜向放置的数轴称为斜轴(记作b轴).类似
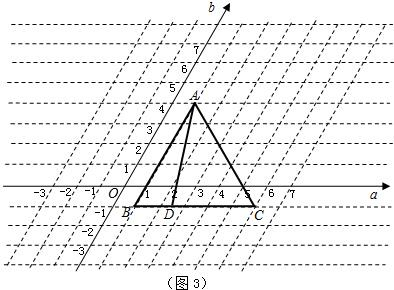
如图1,在平面内取一点O,过点O作两条夹角为60°的数轴,使它们以点O为公共原点且具有相同的单位长度,这样在平面内建立的坐标系称为斜坐标系,我们把水平放置的数轴称为横轴(记作a轴),将斜向放置的数轴称为斜轴(记作b轴).类似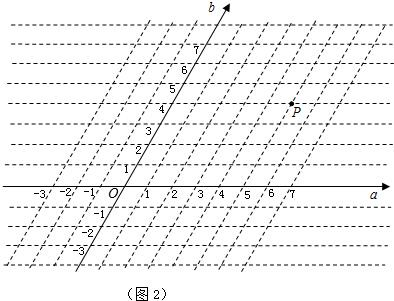
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省淮安市中考模拟试卷2数学试卷(解析版) 题型:解答题
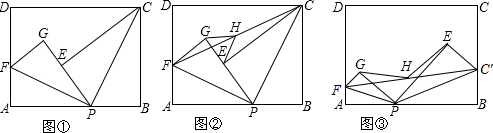
已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(3)如图③,分别在AD、BC上取点F、C’,使得∠APF=∠BPC’,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△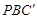 沿
沿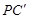 翻折得到△
翻折得到△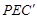 ,连接
,连接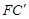 ,取
,取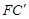 的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com