
【题目】已知:如图,在△ABC中,D、E分别是AB、BC边上的中点,过点C作CF∥AB,交DE的延长线于F点,连接CD、BF.
(1)求证:△BDE≌△CFE;
(2)△ABC满足什么条件时,四边形BDCF是矩形?
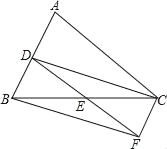
【答案】(1)详见解析;(2)当BC=AC时,四边形BDCF是矩形,理由详见解析
【解析】
(1)由平行线的性质得出∠DBE=∠CFE,由中点的定义得出BE=CE,由ASA证明△BDE≌△CFE即可;
(2)先证明DE是△ABC的中位线,得出DE∥AC,证出四边形BDCF是平行四边形,得出AD=CF,证出CF=BD,得出四边形BDCF是平行四边形;再由等腰三角形的性质得出CD⊥AB,即可得出结论.
(1)证明:∵CF∥AB,
∴∠DBE=∠CFE,
∵E是BC的中点,
∴BE=CE,
在△BDE和△CFE中,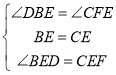
∴△BDE≌△CFE(ASA);
(2)解:当BC=AC时,四边形BDCF是矩形,理由如下:
∵D、E分别是AB,BC的中点
∴DE是△ABC的中位线,
∴DE∥AC,又AF∥BC,
∴四边形BDCF是平行四边形,
∴AD=CF,
又BD=AD,
∴CF=BD,又CF∥BD,
∴四边形BDCF是平行四边形;
∵BC=AC,BD=AD,
∴CD⊥AB,即∠BDC=90°,
∴平行四边形BDCF是矩形.


科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
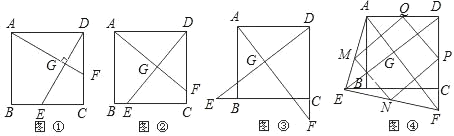
【题目】如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是_________(用代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为_____.
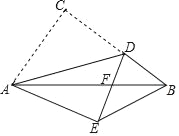
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
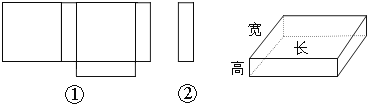
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com