
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

【答案】(1)证明见解析;(2)证明见解析;(3)CN=![]() .
.
【解析】试题分析:
(1)连接OG,则由已知易得∠OGE=∠AHK=90°,由OG=OA可得∠AGO=∠OAG,从而可得∠KGE=∠AKH=∠EKG,这样即可得到KE=GE;
(2)设∠FGB=α,由AB是直径可得∠AGB=90°,从而可得∠KGE=90°-α,结合GE=KE可得∠EKG=90°-α,这样在△GKE中可得∠E=2α,由∠FGB=![]() ∠ACH可得∠ACH=2α,这样可得∠E=∠ACH,由此即可得到CA∥EF;
∠ACH可得∠ACH=2α,这样可得∠E=∠ACH,由此即可得到CA∥EF;
(3)如下图2,作NP⊥AC于P,
由(2)可知∠ACH=∠E,由此可得sinE=sin∠ACH=![]() ,设AH=3a,可得AC=5a,CH=4a,则tan∠CAH=
,设AH=3a,可得AC=5a,CH=4a,则tan∠CAH=![]() ,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC,从而可得CK=AC=5a,由此可得HK=a,tan∠AKH=
,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC,从而可得CK=AC=5a,由此可得HK=a,tan∠AKH=![]() ,AK=
,AK=![]() a,结合AK=
a,结合AK=![]() 可得a=1,则AC=5;在四边形BGKH中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG可得∠ACG=∠AKH,
可得a=1,则AC=5;在四边形BGKH中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG可得∠ACG=∠AKH,
在Rt△APN中,由tan∠CAH=![]() ,可设PN=12b,AP=9b,由tan∠ACG=
,可设PN=12b,AP=9b,由tan∠ACG=![]() tan∠AKH=3可得CP=4b,由此可得AC=AP+CP=
tan∠AKH=3可得CP=4b,由此可得AC=AP+CP=![]() =5,则可得b=
=5,则可得b=![]() ,由此即可在Rt△CPN中由勾股定理解出CN的长.
,由此即可在Rt△CPN中由勾股定理解出CN的长.
试题解析:
(1)如图1,连接OG.
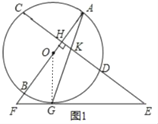
∵EF切⊙O于G,
∴OG⊥EF,
∴∠AGO+∠AGE=90°,
∵CD⊥AB于H,
∴∠AHD=90°,
∴∠OAG=∠AKH=90°,
∵OA=OG,
∴∠AGO=∠OAG,
∴∠AGE=∠AKH,
∵∠EKG=∠AKH,
∴∠EKG=∠AGE,
∴KE=GE.
(2)设∠FGB=α,
∵AB是直径,
∴∠AGB=90°,
∴∠AGE=∠EKG=90°﹣α,
∴∠E=180°﹣∠AGE﹣∠EKG=2α,
∵∠FGB=![]() ∠ACH,
∠ACH,
∴∠ACH=2α,
∴∠ACH=∠E,
∴CA∥FE.
(3)作NP⊥AC于P.
∵∠ACH=∠E,
∴sin∠E=sin∠ACH=![]() ,设AH=3a,AC=5a,
,设AH=3a,AC=5a,
则CH=![]() ,tan∠CAH=
,tan∠CAH=![]() ,
,
∵CA∥FE,
∴∠CAK=∠AGE,
∵∠AGE=∠AKH,
∴∠CAK=∠AKH,
∴AC=CK=5a,HK=CK﹣CH=4a,tan∠AKH=![]() =3,AK=
=3,AK= ![]() ,
,
∵AK=![]() ,
,
∴![]() ,
,
∴a=1.AC=5,
∵∠BHD=∠AGB=90°,
∴∠BHD+∠AGB=180°,
在四边形BGKH中,∠BHD+∠HKG+∠AGB+∠ABG=360°,
∴∠ABG+∠HKG=180°,
∵∠AKH+∠HKG=180°,
∴∠AKH=∠ABG,
∵∠ACN=∠ABG,
∴∠AKH=∠ACN,
∴tan∠AKH=tan∠ACN=3,
∵NP⊥AC于P,
∴∠APN=∠CPN=90°,
在Rt△APN中,tan∠CAH=![]() ,设PN=12b,则AP=9b,
,设PN=12b,则AP=9b,
在Rt△CPN中,tan∠ACN=![]() =3,
=3,
∴CP=4b,
∴AC=AP+CP=13b,
∵AC=5,
∴13b=5,
∴b=![]() ,
,
∴CN=![]() =
= ![]() =
=![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+2,+3,﹣6,﹣1,﹣2,+4.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:+50,﹣15,+25,﹣10,﹣20,则该货车运送的水果总重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
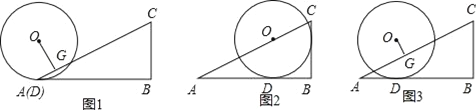
【题目】如图,△ABC中,∠B=90°,tan∠BAC=![]() ,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.
,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.
(1)利用图2,求cos∠BAC的值;
(2)当点D与点A重合时(如图1),求OG;
(3)如图3,在⊙O滚动过程中,设AD=x,请用含x的代数式表示OG,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简再求值:7a2b+(4a2b﹣9ab2)﹣2(5a2b﹣3ab2),其中a=2,b=﹣1.
(2)已知代数式 A=x2+xy﹣2y,B=2x2﹣2xy+x﹣1
①求 2A﹣B.
②若 2A﹣B 的值与 x 的取值无关,求 y 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
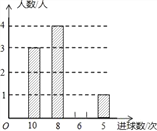
【题目】某校九年级学生在一节体育课中,选一组学生进行投篮比赛,每人投10次,汇总投进球数的情况进行统计分析,绘制了如下不完整的统计表和统计图.
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中选一名学生参加校动会投篮比赛,投进10球的成员被选中的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,淮安动物园在7天假期中每天接待的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数),把9月30日的游客人数记为a万人.
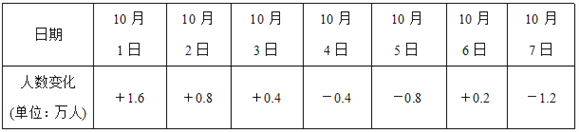
(1)请用含a的代数式表示10月2日的游客人数;
(2)请判断七天内游客人数最多的是哪天,有多少人?
(3)若9月30日的游客人数为2万人,门票每人10元,问黄金周期间淮安动物园门票收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数![]() 与
与![]() (
(![]() )在第一象限图像的性质,经历了如下探究过程:
)在第一象限图像的性质,经历了如下探究过程:
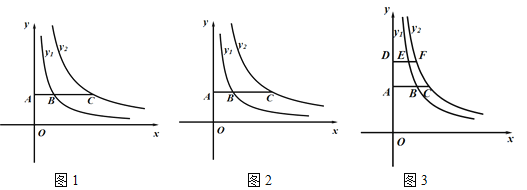
操作猜想:(1)如图1,当![]() ,
,![]() 时,在y轴的正半轴上取一点A作x轴的平行线交
时,在y轴的正半轴上取一点A作x轴的平行线交![]() 于点B,交
于点B,交![]() 于点C.当OA=1时,
于点C.当OA=1时,![]() = ;当OA=3时,
= ;当OA=3时,![]() = ;当OA=a时,猜想
= ;当OA=a时,猜想![]() = .
= .
数学思考:(2)在y轴的正半轴上任意取点A作x轴的平行线,交![]() 于点B、交
于点B、交![]() 于点C,请用含
于点C,请用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用图2加以证明.
的值,并利用图2加以证明.
推广应用:(3)如图3,若![]() ,
,![]() ,在y轴的正半轴上分别取点A、D(OD>OA)作x轴的平行线,交
,在y轴的正半轴上分别取点A、D(OD>OA)作x轴的平行线,交![]() 于点B、E,交
于点B、E,交![]() 于点C、F,是否存在四边形ADFB是正方形?如果存在,求OA的长和点B的坐标;如果不存在,请说明理由.
于点C、F,是否存在四边形ADFB是正方形?如果存在,求OA的长和点B的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com