
【题目】如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是24cm2,求AC的长
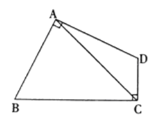
【答案】4![]()
【解析】
过A作AE⊥BC,作AF⊥CD,交CD的延长线于点F,利用三个角为直角的四边形为矩形得到AECF为矩形,利用矩形得四个角为直角得到∠EAF为直角,利用等式的性质得到∠DAF=∠BAE,再由一对直角相等,AB=AD,利用AAS得到三角形ABE与三角形ADF全等,利用全等三角形的对应边相等得到AE=AF,可得出AECF为正方形,三角形ABE面积与三角形AFD面积相等,进而得到四边形ABCD面积等于正方形AECF面积,求出正方形的边长即为AE的长,在等腰直角三角形ACE中,利用勾股定理即可求出AC的长.
解:过A作AE⊥BC,作AF⊥CD,交CD的延长线于点F,
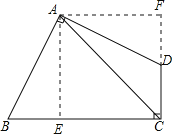
∵∠AEC=∠AFC=∠ECF=90°,
∴四边形AECF为矩形,
∴∠EAF=90°,
∵∠BAD=90°,
∴∠BAE+∠EAD=∠FAD+∠EAD=90°,
∴∠DAF=∠BAE,
在△ABE和△ADF中,
∴△ABE≌△ADF(AAS),
∴AE=AF,S△ABE=S△ADF,
∴四边形AECF是正方形,
∴S四边形ABCD=S正方形AECF=24cm2,
∴AE=2![]() cm,
cm,
∵△AEC为等腰直角三角形,
∴AC=![]() AE=4
AE=4![]() cm.
cm.
故答案为:4![]() .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】如图(1)所示,∠AOB、∠COD都是直角.
(1)试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)若∠BOC=60°,求∠AOD的度数;
(3)猜想∠AOD与∠BOC在数量上是相等,互余,还是互补的关系,并说明理由;
(4)当∠COD绕着点O旋转到图(2)所示位置时,你在(3)中的猜想还成立吗?请用你所学的知识加以说明.
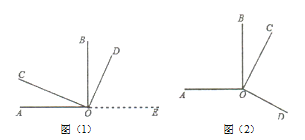
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线OD交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC度数为( ).

A. 108° B. 135° C. 144° D. 160°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )

A.2:5 B.14:25 C.16:25 D.4:21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据 ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣4,﹣3,1,3,4这五个数中,随机抽取一个数,记为m,若m使得关于x,y的二元一次方程组 ![]() 有解,且使关于x的分式方程
有解,且使关于x的分式方程 ![]() ﹣1=
﹣1= ![]() 有正数解,那么这五个数中所有满足条件的m的值之和是( )
有正数解,那么这五个数中所有满足条件的m的值之和是( )
A.1
B.2
C.﹣1
D.﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com