
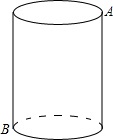
 如图,圆柱高12,底面半径3,一只蚂蚁从A点爬到B点去吃食,要爬行的最短路程是
如图,圆柱高12,底面半径3,一只蚂蚁从A点爬到B点去吃食,要爬行的最短路程是科目:初中数学 来源: 题型:
 小明想将如图所示的一根绳子(无弹性)围成的直角三角形的一个锐角顶点去掉(即把一个锐角顶点变成直角顶点,另两个顶点位置不变).用这条绳子围成一个长方形,那么所围成的长方形的长、宽各是多少?面积是多少?
小明想将如图所示的一根绳子(无弹性)围成的直角三角形的一个锐角顶点去掉(即把一个锐角顶点变成直角顶点,另两个顶点位置不变).用这条绳子围成一个长方形,那么所围成的长方形的长、宽各是多少?面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
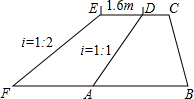 某区为提高某段海堤的防海啸能力,计划修96m长的一堤段(原海堤的横断面如图所示中的梯形ABCD)的堤面加宽1.6m,背水坡比由原来的1:1改为1:2,已知背水坡长AD=8.0m,求完成这一工程所需的土方(要求保留两个有效数字,本题可能使用的数据
某区为提高某段海堤的防海啸能力,计划修96m长的一堤段(原海堤的横断面如图所示中的梯形ABCD)的堤面加宽1.6m,背水坡比由原来的1:1改为1:2,已知背水坡长AD=8.0m,求完成这一工程所需的土方(要求保留两个有效数字,本题可能使用的数据| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 25 |
| 3 |
| 3 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| A、等腰三角形底边上的高所在的直线是对称轴 |
| B、等腰三角形底边上的中线所在的直线是对称轴 |
| C、等腰三角形顶角的平分线所在的直线是对称轴 |
| D、等腰三角形一内角平分线所在的直线是对称轴 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| P(P-a)(P-b)(P-c) |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com