
【题目】 明德中学在商场购买甲、乙两种不同足球,购买甲种足球共花费3000元,购买乙种足球共花费2100元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)为响应国家“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%.如果此次购买甲、乙两种足球的总费用不超过2950元,那么这所学校最多可购买多少个乙种足球?
【答案】(1)购买一个甲种足球需要50元,购进一个乙种足球需要70元;(2)这所学校最多可购买25个乙种足球.
【解析】
(1)设购买一个甲种足球需要x元,则购进一个乙种足球需要![]() 元,根据数量=总价÷单价结合3000元购买的甲种足球数量是2100元购买的乙种足球数量的2倍,即可得出关于x的分式方程,解之经检验后即可得出结论;
元,根据数量=总价÷单价结合3000元购买的甲种足球数量是2100元购买的乙种足球数量的2倍,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设这所学校可购买m个乙种足球,则购买![]() 个甲种足球,根据总价=单价×数量结合总费用不超过2950元,即可得出关于m的一元一次不等式,解之取其中的最大值即可得出结论.
个甲种足球,根据总价=单价×数量结合总费用不超过2950元,即可得出关于m的一元一次不等式,解之取其中的最大值即可得出结论.
(1)设购买一个甲种足球需要x元,则购进一个乙种足球需要![]() 元
元
依题意得:![]()
解得:![]()
经检验,![]() 是所列分式方程的解,且符合题意
是所列分式方程的解,且符合题意
此时,![]()
答:购买一个甲种足球需要50元,购进一个乙种足球需要70元;
(2)设这所学校可购买m个乙种足球,则购买![]() 个甲种足球,
个甲种足球,
依题意得:![]()
解得:![]()
答:这所学校最多可购买25个乙种足球.


科目:初中数学 来源: 题型:
【题目】高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资,已知生产每件产品的成本是40元.在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利(年获利=年销售额一生产成本—投资)为z(万元).
(1)试写出y与x之间的函数关系式(不写x的取值范围);
(2)试写出z与x之间的函数关系式(不写x的取值范围);
(3)公司计划,在第一年按年获利最大确定销售单价进行销售;到第二年年底获利不低于1130万元,请借助函数的大致图象说明:第二年的销售单价x(元)应确定在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足△BCP的周长为14cm,求此时t的值;
(2)若点P在∠BAC的平分线上,求此时t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的面积为32,对角线BD绕着它的中点O按顺时针方向旋转一定角度后,其所在直线分别交BC,AD于点E、F,若AF=3DF,则图中阴影部分的面积等于_____

查看答案和解析>>
科目:初中数学 来源: 题型:
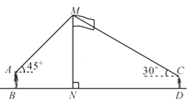
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7 m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(0,b),且a、b满足(a﹣2)2+![]() =0.
=0.

(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,且△ABM是等腰直角三角形,求m值;
(3)过A点的直线y=kx﹣2k交y轴于负半轴于P,N点的横坐标为﹣1,过N点的直线y=![]() x﹣
x﹣![]() 交AP于点M,试证明
交AP于点M,试证明![]() 的值为定值.
的值为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
对于二次三项式![]() 可以直接分解为
可以直接分解为![]() 的形式,但对于二次三项式
的形式,但对于二次三项式![]() ,就不能直接用公式了,我们可以在二次三项式
,就不能直接用公式了,我们可以在二次三项式![]() 中先加上一项
中先加上一项![]() ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去![]() 这项,(这里也可把
这项,(这里也可把![]() 拆成
拆成![]() 与
与![]() 的和),使整个式子的值不变.
的和),使整个式子的值不变.
于是有:![]()
![]()
![]()
![]()
![]()
![]() ,
,
我们把像这样将二次三项式分解因式的方法叫做添(拆)项法.
(应用材料)
![]() 上式中添(拆)项后先把完全平方式组合在一起,然后用______法实现分解因式.
上式中添(拆)项后先把完全平方式组合在一起,然后用______法实现分解因式.
![]() 请你根据材料中提供的因式分解的方法,将下面的多项式分解因式:
请你根据材料中提供的因式分解的方法,将下面的多项式分解因式:
![]() ;
;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )

A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com