【答案】分析:令x=1求出a+a1+a2+a3+a4+a5+a6+a7+a8+a9的值,令x=-1求出a-a1+a2-a3+a4-a5+a6-a7+a8-a9的值,再根据平方差公式展开,然后代入计算即可得解.
解答:解:令x=1,则a+a1+a2+a3+a4+a5+a6+a7+a8+a9=(2×1-1)9=1,①
令x=-1,则a-a1+a2-a3+a4-a5+a6-a7+a8-a9=[2×(-1)-1]9=-39,②
所以,(a+a2+a4+a6+a8)2-(a1+a3+a5+a7+a9)2=(a+a1+a2+a3+a4+a5+a6+a7+a8+a9)(a-a1+a2-a3+a4-a5+a6-a7+a8-a9)=1×(-39)=-39.
故答案为:-39.
点评:本题考查了函数值的求解,根据脚码的偶数与奇数特点,令x=1与x=-1,分别求出相应的值是解题的关键.

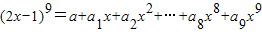 ,则
,则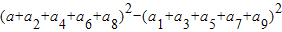 的值为 .
的值为 . 
