
【题目】完成证明并写出推理根据: 已知,如图,∠1=132°,∠ACB=48°,∠2=∠3,FH⊥AB于H.
求证:CD⊥AB.
证明:∵∠1=132°,∠ACB=48°,
∴∠1+∠ACB=180°
∴DE∥BC
∴∠2=()
又∵∠2=∠3
∴∠3=∠DCB
∴HF∥()
∴∠CDB= . ()
又∵FH⊥AB,
∴∠FHB=()
∴∠CDB=°.
∴CD⊥AB.()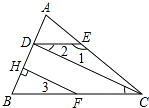
【答案】∠DCB;两直线平行,内错角相等;CD;同位角相等,两直线平行;∠FHB;两直线平行,同位角相等;90°;垂直定义;90;垂直定义
【解析】证明:∵∠1=132°,∠ACB=48°, ∴∠1+∠ACB=180°,
∴DE∥BC,
∴∠2=∠DCB(两直线平行,内错角相等),
又∵∠2=∠3,
∴∠3=∠DCB,
∴HF∥CD(同位角相等,两直线平行),
∴∠CDB=∠FHB,(两直线平行,同位角相等),
又∵FH⊥AB,
∴∠FHB=90°(垂直定义),
∴∠CDB=90°,
∴CD⊥AB(垂直定义),
所以答案是:∠DCB,两直线平行,内错角相等,CD,同位角相等,两直线平行,∠FHB,两直线平行,同位角相等,90°,垂直定义,90,垂直定义.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】定义新运算:对于任意实数a,b都有:a⊕b=a(a﹣b)+1,其中等式右边是通常的加法、减法及乘法运算.如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么方程3⊕x=13的解为x=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一动点,CE⊥BD于E.

(1)如图(1),若BD平分∠ABC时,①求∠ECD的度数;②延长CE交BA的延长线于点F,补全图形,探究BD与EC的数量关系,并证明你的结论;
(2)如图(2),过点A作AF⊥BE于点F,猜想线段BE,CE,AF之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截止到3月26日0时,全球感染新型冠状病毒肺炎的人数已经突破380000人,“山川异域,风月同天”,携手抗“疫”,刻不容缓.将380000用科学记数法表示为( )
A.0.38×106B.3.8×106C.3.8×105D.38×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是某校九年级10名同学参加学校演讲比赛的统计表,则这组数据的众数和中位数分别为()
成绩/分 | 80 | 85 | 90 | 95 |
人数/人 | 1 | 3 | 4 | 2 |
A.90,87.5B.85,84C.85,90D.90,90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
点C与点F分别是对应点,观察点与点的坐标之间的关系,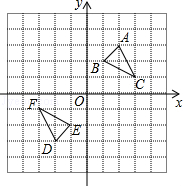
解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 点
点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为![]() 秒.
秒.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)以点![]() 为圆心,
为圆心,![]() 为半径的
为半径的![]() 随点
随点![]() 的运动而变化,当
的运动而变化,当![]() 与四边形
与四边形![]() 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求![]() 的值.
的值.
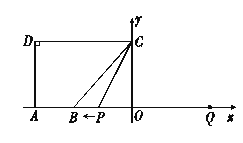
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com