
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )

A.①②③ B.①②④ C.②③④ D.①③④
【答案】A
【解析】
试题分析:由AB的垂直平分线DE交AC于D,交AB于E,可得AD=BD,即可求得∠ABD=∠A=36°,又由AB=AC,即可求得∠CBD=∠ABD=36°,∠BDC=∠C=72°,继而证得AD=BD=BC,△BDC的周长等于AB+BC.
解:∵AB的垂直平分线DE交AC于D,交AB于E,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∴∠CBD=∠ABD=36°,
即BD平分∠ABC;故①正确;
∴∠BDC=∠C=72°,
∴BC=BD,
∴BC=BD=AD,故②正确;
∴△BDC的周长为:BC+CD+BD=BC+C+AD=AC+BC=AB+BC;故③正确;
∵CD<BD,
∴CD<AD,
∴D不是AC中点.故④错误.
故选A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为“厉行节能减排,倡导绿色出行”,某公司拟在我县甲、乙两个街道社区试点投放一批共享单车(俗称“小黄车”),这批自行车包括A、B两种不同款型,投放情况如下表:
成本单价 (单位:元) | 投放数量(单位:辆) | 总价(单位:元) | |
A型 |
| 50 | 50 |
B型 |
| 50 |
|
成本合计(单位:元) | 7500 | ||
(1)根据表格填空:
本次试点投放的A、B型“小黄车”共有 辆;用含有![]() 的式子表示出B型自行车的成本总价为 ;
的式子表示出B型自行车的成本总价为 ;
(2)试求A、B两种款型自行车的单价各是多少元?
(3)经过试点投放调查,现在该公司决定采取如下方式投放A型“小黄车”:甲街区每100人投放n辆,乙街区每100人投放(n+2)辆,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有![]() 人,求甲街区每100人投放A型“小黄车”的数量.
人,求甲街区每100人投放A型“小黄车”的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=______cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为4的顶点开始,第2018次“移位”后,那么他所处的顶点的编号是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
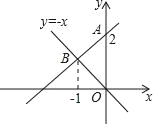
【题目】如图,一次函数图象经过点A(0,2),且与正比例函数y=﹣x的图象交于点B,B点的横坐标是﹣1.
(1)求该一次函数的解析式:
(2)求一次函数图象、正比例函数图象与x轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是BC边上的高,点E是AC边的中点,点P是AD上的一个动点,当PC+PE最小时,∠CPE的度数是( )

A.30°B.45°C.60°D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用三种大小不同的六个正方形 和一个缺角的正方形拼成长方形 ABCD, 其中,GH=2cm, GK=2cm, 设 BF=x cm,

(1)用含 x 的代数式表示 CM= _______cm, DM=_______ cm.
(2)若 x=2cm,求长方形 ABCD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,三角形ABC的顶点坐标分别是A(0,0),B(5,0),C(4,4).
(1)将三角形ABC向上平移2个单位长度,再向右平移3个单位长度,得到三角形A1B1C1,请在直角坐标系中画平移后的三角形A1B1C1
(2)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com