
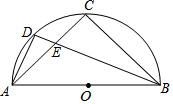
 如图,AB是半圆O的直径,C是$\widehat{AB}$的中点,D是$\widehat{AC}$的中点,AC与BD相交于点E.
如图,AB是半圆O的直径,C是$\widehat{AB}$的中点,D是$\widehat{AC}$的中点,AC与BD相交于点E.分析 (1)D是$\widehat{AC}$的中点,由圆周角定理可知:∠ABD=∠CBD,所以BD平分∠ABC;
(2)延长BC与AD相交于点F,易证△BCE≌△ACF(ASA),从而可知BE=AF,在证明AB=BF,从而可证明BE=2AD;
(3)连接OD,交AC于H.设OH为1,则BC为2,OB=OD=$\sqrt{2}$,DH=$\sqrt{2}-1$,从而可知$\frac{DE}{BE}$=$\frac{{\sqrt{2}-1}}{2}$
解答 解:(1)∵D是$\widehat{AC}$的中点,
∴由圆周角定理可知:∠ABD=∠CBD
∴BD平分∠ABC
(2)延长BC与AD相交于点F,
∵C是$\widehat{AB}$的中点,
∴AC=BC,
由(1)可知:∠FAC=∠CBE,
∵AB是直径,
∴∠ADB=∠ACB=90°,
在△BCE与△ACF中,
$\left\{\begin{array}{l}{∠FAC=∠CBE}\\{AC=BC}\\{∠FCA=∠BCE}\end{array}\right.$
∴△BCE≌△ACF(ASA),
∴BE=AF,
∵BD平分∠ABC,BD⊥AF,
∴AB=BF,
∴D是AF的中点,
∴BE=AF=2AD (3)连接OD,交AC于H.
(3)连接OD,交AC于H.
∵D是$\widehat{AC}$的中点,
∴由垂径定理可知:OD⊥AC,
∵O是AB的中点,
∴OH是△ABC的中位线,
设OH为1,则BC为2,
∴由勾股定理可知:AB=2$\sqrt{2}$
∴OB=OD=$\sqrt{2}$,
∴DH=$\sqrt{2}-1$,
∵OH∥BC,
∴△DEH∽△BCE
∴$\frac{DE}{BE}$=$\frac{DH}{BC}$
∴$\frac{DE}{BE}$=$\frac{{\sqrt{2}-1}}{2}$
点评 本题考查圆的综合问题,涉及相似三角形的判断与性质,全等三角形的判定与性质,勾股定理等知识,属于中等题型.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +5 | +3.5 | -1 | -2.5 | -5.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…,则正方形OBn-1BnCn的顶点Bn的坐标是当k为自然数,如果n=8k+1时,那么Bn(24k,24k);如果n=8k+2时,那么Bn(0,24k+1);如果n=8k+3时,那么Bn(-24k+1,24k+1);如果n=8k+4时,那么Bn(-24k+2,0);如果n=8k+5时,那么Bn(-24k+2,-24k+2);如果n=8k+6时,那么Bn(0,-24k+3);如果n=8k+7时,那么Bn(24k+3,-24k+3);如果n=8k+8时,那么Bn(24k+4,0)..
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…,则正方形OBn-1BnCn的顶点Bn的坐标是当k为自然数,如果n=8k+1时,那么Bn(24k,24k);如果n=8k+2时,那么Bn(0,24k+1);如果n=8k+3时,那么Bn(-24k+1,24k+1);如果n=8k+4时,那么Bn(-24k+2,0);如果n=8k+5时,那么Bn(-24k+2,-24k+2);如果n=8k+6时,那么Bn(0,-24k+3);如果n=8k+7时,那么Bn(24k+3,-24k+3);如果n=8k+8时,那么Bn(24k+4,0)..查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,圆的半径为2,圆的两条弦AB,CD互相垂直,垂足为E.若圆心O到弦AB的距离OF=1,EF=1.则图中阴影部分的面积等于7.23(π取3.14)
如图所示,圆的半径为2,圆的两条弦AB,CD互相垂直,垂足为E.若圆心O到弦AB的距离OF=1,EF=1.则图中阴影部分的面积等于7.23(π取3.14)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请把下面证明过程补充完整
请把下面证明过程补充完整查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 实际每天比计划多完成改造任务300m,实际所用天数是计划的$\frac{2}{3}$ | |
| B. | 实际每天比计划少完成改造任务300m,计划所用天数是实际的$\frac{2}{3}$ | |
| C. | 实际每天比计划多完成改造任务300m,计划所用天数是实际的$\frac{2}{3}$ | |
| D. | 实际每天比计划少完成改造任务300m,实际所用天数是计划的$\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com