【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象交x轴于（-1，0）点，则下列结论中正确的是（ ）
A.c＜0B.a-b+c<0C.b2<4acD.2a+b=0
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在直角三角形中，除直角外的5个元素中，已知2个元素（其中至少有1个是边），就可以求出其余的3个未知元素.对于任意三角形，我们需要知道几个元素就可以求出其余的未知元素呢？思考并解答下列问题：
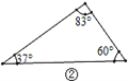
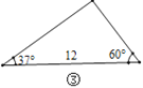
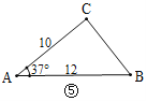
（1）观察图①~图④，根据图中三角形的已知元素，可以求出其余未知元素的序号是____.
（2）如图⑤，在
中，已知
，
，
，能否求出BC的长度？如果能，请求出BC的长度；如果不能，请说明理由.（参考数据：
，
，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形
中，
、
分别是
、
的中点，连接
、
、
、
，且
.
（1）求证：
；
（2）若
，求的长；
（3）在（2）的条件下，求出
的外接圆圆心与
的外接圆圆心之间的距离？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】水务部门为加强防汛工作，决定对马边河上某电站大坝进行加固．原大坝的横断面是梯形ABCD，如图所示，已知迎水面AB的长为20米，∠B＝60°，背水面DC的长度为20
米，加固后大坝的横断面为梯形ABED．若CE的长为5米．
（1）已知需加固的大坝长为100米，求需要填方多少立方米；
（2）求新大坝背水面DE的坡度．（计算结果保留根号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ACB中，∠C=90°，AC=3，BC=4，O是BC的中点，到点O的距离等于
BC的所有点组成的图形记为G，图形G与AB交于点D．
（1）补全图形并求线段AD的长；
（2）点E是线段AC上的一点，当点E在什么位置时，直线ED与 图形G有且只有一个交点？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，AC，BC分別与⊙O交于点D，E，则下列说法一定正确的是（ ）
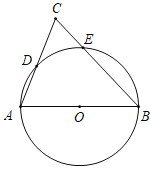
A.连接BD，可知BD是△ABC的中线B.连接AE，可知AE是△ABC的高线
C.连接DE，可知
D.连接DE，可知S△CDE：S△ABC＝DE：AB
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，菱形ABCD中，∠B＝60°，AB＝3cm，过点A作∠EAF＝60°，分别交DC，BC的延长线于点E，F，连接EF．
（1）如图1，当CE＝CF时，判断△AEF的形状，并说明理由；
（2）若△AEF是直角三角形，求CE，CF的长度；
（3）当CE，CF的长度发生变化时，△CEF的面积是否会发生变化，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P是直径AB上的一点，AB=6，CP⊥AB交半圆
于点C，以BC为直角边构造等腰Rt△BCD，∠BCD=90°，连接OD．
小明根据学习函数的经验，对线段AP，BC，OD的长度之间的关系进行了探究．
下面是小明的探究过程，请补充完整：
（1）对于点P在AB上的不同位置，画图、测量，得到了线段AP，BC，OD的长度的几组值，如下表：
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP，BC，OD的长度这三个量中，确定________的长度是自变量，________的长度和________的长度都是这个自变量的函数；
（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；
（3）结合函数图象，解决问题：当OD=2BC时，线段AP的长度约为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC内接于⊙O，∠B=600，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．
（1）求证：PA是⊙O的切线；
（2）若PD=
，求⊙O的直径．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
