
【题目】在平面直角坐标系中,已知两点A(-4,0)、B(1,0),且以AB为直径的圆交![]() 轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.
轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.

(1)求过A, B,C三点的抛物线解析式;
(2)求点D的坐标;
(3)设平行于x轴的直线交抛物线于E,F两点,问是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.
【答案】(1)![]() ;(2)D的坐标为(
;(2)D的坐标为(![]() ,0);(3)存在,
,0);(3)存在, ![]() 或
或![]() .
.
【解析】(1)已知了抛物线过A,B,C三点,可根据三点的坐标用待定系数法求出抛物线的解析式.
(2)由于CD是圆的切线,设圆心为O′,可连接O′C,在直角三角形O′CD中科根据射影定理求出OD的长,即可得出D的坐标.
(3)可假设存在这样的点E、F,设以线段EF为直径的圆的半径为|r|,那么可用半径|r|表示出E,F两点的坐标,然后根据E,F在抛物线上,将E,F的坐标代入抛物线的解析式中,可得出关于|r|的方程,如果方程无解则说明不存在这样的E,F点,如果方程有解,可用得出的r的值求出E,F两点的坐标.
解:(1)设二次函数的解析式为![]() ,则
,则
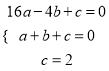 ,
,  ,
,
故抛物线的解析式为![]() .
.
过圆心O′做抛物线的对称轴,连接O′C.
(2)如图所示,
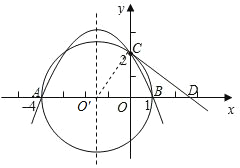
以![]() 为直径的圆圆心坐标为O′(
为直径的圆圆心坐标为O′(![]() ,0).
,0).
![]() ,
, ![]() .
.
∵CD为⊙O′切线
∴O′C⊥CD,
∵ ∠O′OC=∠COD=90°
∴ ∠CDO+∠DCO=∠CDO+∠CO′O=90°
∴ ∠DCO=∠CO′O
∴ ⊿O′CO∽⊿CDO, ![]() ,
,
∴ ,
,
![]() .
.
∴ D的坐标为(![]() ,0).
,0).
(3)存在.抛物线对称轴为![]() .设圆的半径为r(r>0),令点
.设圆的半径为r(r>0),令点![]() 在点F的左边.
在点F的左边.
①当E,F在![]() 轴上方时,则E坐标为(
轴上方时,则E坐标为(![]() -r,r),F坐标为(
-r,r),F坐标为(![]() +r,r)将点E坐标代入抛物线
+r,r)将点E坐标代入抛物线
![]() 中,得r=
中,得r=![]() (
(![]() -r)2-
-r)2-![]() (-
(-![]() -r)+2,
-r)+2,
![]() ,
, ![]() (舍去).
(舍去).
②当E,F在x轴下方时,则E坐标为(-![]() -r,-r),F坐标为(-
-r,-r),F坐标为(-![]() +r,-r),将E点的坐标代入
+r,-r),将E点的坐标代入![]() .得-r=-(-
.得-r=-(-![]() -r)2-
-r)2-![]() (-
(-![]() -r)+2,得r3=1+
-r)+2,得r3=1+![]() 或r4=1-
或r4=1-![]() (舍去) .
(舍去) .
故在以![]() 为直径的圆,恰好与
为直径的圆,恰好与![]() 轴相切,该圆的半径为
轴相切,该圆的半径为![]() 或
或![]() .
.
“点睛”本题着重考查了待定系数法求二次函数解析式、三角形相似、切线的性质等重要知识点,综合性强,考查学生数形结合的数学思想方法.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点,如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,当点Q的运动速度为时,能够在某一时刻使△BPD与△CQP全等. 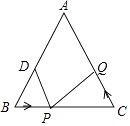
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地的距离是80千米,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,已知小汽车比公共汽车迟20分钟到达B地,求两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】角平分线上的点到角两边的距离相等.这一性质在解决图形面积问题时有何妙用呢?阅读材料:已知,如图(1),在面积为S的△ABC中,BC=a,AC=b,AB=c,三条角平分线的交点O到三边的距离为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△OAC+S△OAB= ![]() BCr+
BCr+ ![]() ACr+
ACr+ ![]() ABr=
ABr= ![]() (a+b+c)r,∴r=
(a+b+c)r,∴r= ![]()

(1)类比推理:若面积为S的四边形ABCD的四条角平分线交于O点,如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求点O到四边的距离r;
(2)理解应用:如图(3),在四边形ABCD中,AB∥DC,AB=21,CD=11,AD=BC=13,对角线BD=20,点O1与O2分别为△ABD与△BCD的三条角平分线的交点,设它们到各自三角形三边的距离为r1和r2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c的图象经过点(﹣1,0)和(3,0),则方程ax2+bx+c=0的解为( )
A.x1=﹣3,x2=﹣1B.x1=1,x2=3
C.x1=﹣1,x2=3D.x1=﹣3,x2=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中不可以判定两个直角三角形全等的是( )
A. 两条直角边对应相等 B. 斜边和直角边对应相等
C. 一条边和一锐角对应相等 D. 两个角对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm. 
(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com