
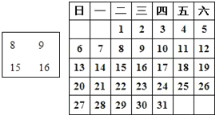
����Ŀ�����±ߵ������У���һ������������Ȧ�����ж����ĸ�����
��

���ڵ�һ�е�һ�е��Ǹ�����ʾΪ![]() ����������ֱ�Ϊ
����������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
��1���ֱ��ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��![]() ��
��![]() ����������
����������![]() =��������.
=��������.![]() =������������
=������������![]() =������������.
=������������.
��2�������ĸ����ĺͣ��ú�![]() �Ĵ���ʽ��ʾ��Ҫ��ϲ�ͬ�����
�Ĵ���ʽ��ʾ��Ҫ��ϲ�ͬ�����
��3�����ĸ����ĺͻ����48������ᣬ�������ʱ![]() ��ֵ��������ᣬ˵�����ɣ���Ҫ���з��̽��
��ֵ��������ᣬ˵�����ɣ���Ҫ���з��̽��
��4�����ĸ����ĺͻ����112������ᣬ�������ʱ![]() ��ֵ��������ᣬ˵�����ɣ���Ҫ���з��̽��
��ֵ��������ᣬ˵�����ɣ���Ҫ���з��̽��
���𰸡���1��![]() .
.![]() .
.![]() ����2��
����2��![]() ;��3���ᣬ
;��3���ᣬ![]() ���������;��4�����ĸ����ĺͲ������112���������.
���������;��4�����ĸ����ĺͲ������112���������.
��������
��1���۲����������ҳ����ұߵ�������ߵ�����1��������������������7������ڵڶ��еڶ��е��Ǹ�����ʾΪa�������ú�a�Ĵ���ʽ��ʾ��b��c��d��
��2�����ĸ�����ӣ����ɵó����ۣ�
��3���������ĸ����ĺ͵���48�����ݣ�2���Ľ��ۿɵó�����a��һԪһ�η��̣���֮�������aֵ����aΪ����������������ɵó�����������Ӷ��ó����ĸ����ĺͻ����48��
��4���������ĸ����ĺ͵���112�����ݣ�2���Ľ��ۿɵó�����a��һԪһ�η��̣���֮�������aֵ����һ�����c=32������c=32���������ϵ�������������ɵó����費�������Ӷ��ó����ĸ����ĺͲ������112��
��1���ڵ�һ�е�һ�е���Ϊ![]() ��������3�����ֱ���
��������3�����ֱ���![]() ��
��![]() ��
��![]() ��
��
��2��![]() =
=![]() ��
��
��3���������ĸ����ĺ͵���48���ɣ�2���ã�
![]() ��
��
���![]() ��
��
��Ϊ![]() �������������ʵ�ʣ����ԣ�4�����ĺ��ܵ���48.
�������������ʵ�ʣ����ԣ�4�����ĺ��ܵ���48.
��4���������ĸ����ĺ͵���112���ɣ�2���ã�
![]() ��
��
���![]() ��
��![]() ���������⣩��
���������⣩��
�����ĸ����ĺͲ������112��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y��![]() ��ͼ�����������㣨2��y1������3��y2��������1��y3������y1��y2��y3�Ĵ�С��ϵ�ǣ�������
��ͼ�����������㣨2��y1������3��y2��������1��y3������y1��y2��y3�Ĵ�С��ϵ�ǣ�������
A. y1��y2��y3B. y2��y1��y3C. y3��y1��y2D. y3��y2��y1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ��
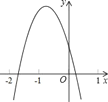
���н��ۣ���abc��0����2a��b��0����4a��2b+c��0������a+c��2��b2������ȷ�ĸ����У�������
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֱ��![]() ��ͼ������������⣺
��ͼ������������⣺
(1)������ͼ����y�ᡢx��ֱ��ڵ�A��B����AB�ij���
(2)��![]() ���ܳ�(OΪ����ԭ��)��
���ܳ�(OΪ����ԭ��)��
(3)���O��ֱ��AB�ľ��룻
(4)��![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E��F�ֱ���AB��BC�ϣ���AE=BF=1��CE��DF���ڵ�O�����н��ۣ��١�DOC=90�㣬��OC=OE����CE=DF����tan��OCD=![]() ����S��DOC=S�ı���EOFB�У���ȷ���У�������
����S��DOC=S�ı���EOFB�У���ȷ���У�������
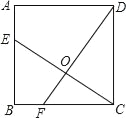
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC ��λ����ͼ��ʾ����ÿ��С�����DZ߳�Ϊ 1 ����λ���ȵ������Σ�
��1������ABC �� y �᷽������ƽ�� 4 ����λ���ȵõ�![]() ���
��� ![]() ����Ϊ_______��
����Ϊ_______��
��2������ABC ���ŵ� O ��ʱ����ת 90����������ת��õ���![]() ��
��
��3��ֱ��д����![]() ��
��![]() �����꣮
�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=2x+4
��1������ͼ��ʾ��ƽ��ֱ������ϵ�У�����������ͼ��

2����ͼ����x��Ľ���A�����꣬��y�ύ��B�����ꣻ
��3���ڣ�2���������£������AOB�������
��4������ͼ��ֱ��д������y��0ʱ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������ϣ�������⣺
���壺�ڷ�ʽ�У�����ֻ����һ����ĸ�ķ�ʽ�������ӵĴ���С�ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ�����ʽ�����磺![]() �������ķ�ʽ�������ʽ�������ӵĴ������ڻ���ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ���ٷ�ʽ�����磺
�������ķ�ʽ�������ʽ�������ӵĴ������ڻ���ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ���ٷ�ʽ�����磺![]() �����ķ�ʽ���Ǽٷ�ʽ���ٷ�ʽҲ���Ի�Ϊ����ʽ��������ʽ�����ʽ�ĺ͵���ʽ����
�����ķ�ʽ���Ǽٷ�ʽ���ٷ�ʽҲ���Ի�Ϊ����ʽ��������ʽ�����ʽ�ĺ͵���ʽ����
�磺![]() ��
��
��1����ʽ![]() ���� �����������ʽ�������ٷ�ʽ������
���� �����������ʽ�������ٷ�ʽ������
��2�����ٷ�ʽ![]() �ֱ�Ϊ����ʽ��
�ֱ�Ϊ����ʽ��
��3�������ʽ![]() ��ֵΪ�����������з�������������x��ֵ��
��ֵΪ�����������з�������������x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿ�����ˮ��ʶ����������ˮ��Դ��ij�в����������շ����������±���
��ˮ�� | ���� |
���۲����� | 2Ԫ |
���� | 4Ԫ |
���� |
|
�磺ij�û�![]() �·���ˮ
�·���ˮ![]() ����Ӧ��ˮ�ѣ�
����Ӧ��ˮ�ѣ�![]() (Ԫ)
(Ԫ)
��1��ij�û�![]() ����ˮ
����ˮ![]() Ӧ��ˮ��____________Ԫ��
Ӧ��ˮ��____________Ԫ��
��2����֪ij�û�![]() �·ݽ�ˮ��
�·ݽ�ˮ��![]() Ԫ������û�
Ԫ������û�![]() �·ݵ���ˮ����
�·ݵ���ˮ����
��3��������û�![]() ��
��![]() �·ݹ���ˮ
�·ݹ���ˮ![]() (
(![]() �·���ˮ������
�·���ˮ������![]() �·���ˮ��)������ˮ��
�·���ˮ��)������ˮ��![]() Ԫ����û�����
Ԫ����û�����![]() ��
��![]() �·ݸ���ˮ����
�·ݸ���ˮ����![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com