
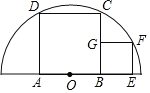
【题目】正方形ABCD、正方形BEFG,点A、B、E在半圆O的直径上,点D、C、F在半圆O上,若EF=4,则该半圆的半径为( )
A.![]() B.8C.
B.8C.![]() D.
D.![]()
【答案】A
【解析】
先根据正方形的性质得CB=AB,AB=2OB=2OA,设OB=x,则OE=x+4,BC=2x,再根据勾股定理,在Rt△COB中有OC2=OB2+CB2=5x2,在Rt△OEF中有OF2=OE2+EF2=(x+4)2+42,则(x+4)2+42=5x2,然后解方程得到x=4,再利用CO=![]() x进行计算即可.
x进行计算即可.
解:如图,连接OD、OC、OF,

∵四边形ABCD为正方形,
∴CB=AB,AB=2OB=2OA,
设OB=x,则OE=x+4,CB=2x,
在Rt△CBO中,OC2=OB2+CB2=x2+(2x)2=5x2,
在Rt△OEF中有OF2=OE2+EF2=(x+4)2+42,
而OC=OF,
∴(x+4)2+42=5x2,
整理得x2﹣2x﹣8=0,
解得x1=4,x2=﹣2(舍去),
∴OC=![]() x=4
x=4![]() ,
,
即该圆的半径为4![]() .
.
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的两个动点,且
上的两个动点,且![]() ,过点
,过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() 的垂线相交于点
的垂线相交于点![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .有以下结论:①
.有以下结论:①![]() ;②当点
;②当点![]() 与点
与点![]() 重合时,
重合时,![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学选拔一名青年志愿者:经笔试、面试,结果小明和小丽并列第一.评委会决定通过抓球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球,小明先取出一个球,记住颜色后放回,然后小丽再取出一个球.若两次取出的球都是红球,则小明胜出;若两次取出的球是一红一绿,则小丽胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
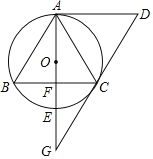
【题目】如图,菱形ABCD,∠D=60°,△ABC内接于⊙O,⊙O的直径AE交BC于F,DC的延长线交AE的延长线于点G.
(1)求证:DG与⊙O相切;
(2)连接DF,求tan∠FDC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
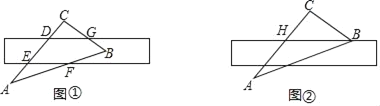
【题目】将直尺摆放在三角板上,使直尺与三角板的边分别交于点D、E、F、G,如图①所示.已知∠CGD=42.
(1)求∠CEF的度数.
(2)将直尺向下平移,使直尺的边缘通过点B,交AC于点H,如图②所示.点H、B的读数分别为4、13.4,求BC的长(精确到0.1)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
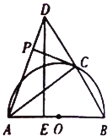
【题目】如图,已知![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() ,半径
,半径![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,点
,点![]() 的对应点为
的对应点为![]() ,当点
,当点![]() 与点
与点![]() 重合时停止.连接
重合时停止.连接![]() 并延长到点
并延长到点![]() ,使得
,使得![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() ______;
______;
(2)如图,当点![]() 与点
与点![]() 重合时,判断
重合时,判断![]() 的形状,并说明理由;
的形状,并说明理由;

(3)如图,当![]() 时,求
时,求![]() 的长;
的长;

(4)如图,若点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,当
,当![]() 与半圆
与半圆![]() 相切时,直接写出直线
相切时,直接写出直线![]() 与
与![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD.
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求AF的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com