
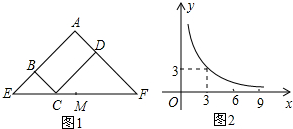
分析 由于等腰直角三角形AEF的斜边EF过C点,则△BEC和△DCF都是直角三角形;观察反比例函数图象得反比例解析式为y=$\frac{9}{x}$;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3$\sqrt{2}$,CF=3$\sqrt{2}$,则C点与M点重合;当y=9时,根据反比例函数的解析式得x=1,即BC=1,CD=9,所以EF=10$\sqrt{2}$,而EM=5$\sqrt{2}$;由于EC•CF=$\sqrt{2}$x×$\sqrt{2}$y;利用等腰直角三角形的性质BE•DF=BC•CD=xy,然后再根据反比例函数的性质得BE•DF=9,其值为定值.
解答 解:因为等腰直角三角形AEF的斜边EF过C点,M为EF的中点,所以△BEC和△DCF都是直角三角形;
观察反比例函数图象得x=3,y=3,则反比例解析式为y=$\frac{9}{x}$;
①、当x=3时,y=3,即BC=CD=3,所以CE=$\sqrt{2}$BC=3$\sqrt{2}$,CF=$\sqrt{2}$CD=3$\sqrt{2}$,C点与M点重合,则EC=EM,所以①错误;
②、当y=9时,x=1,即BC=1,CD=9,所以EC=$\sqrt{2}$,EF=10$\sqrt{2}$,EM=5$\sqrt{2}$,所以②错误;
③、因为EC•CF=$\sqrt{2}$x•$\sqrt{2}$y=2×xy=18,所以,EC•CF为定值,所以③错误;
④、因为BE•DF=BC•CD=xy=9,即BE•DF的值不变,所以④正确.
故答案为:④.
点评 本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
已知二次函数y=ax2+bx+2,它的图象经过点(1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
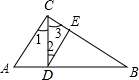 如图,在Rt△ABC中,AC⊥BC,CD⊥AB,∠1=∠2,有下列结论:(1)AC∥DE;(2)∠A=∠3;(3)∠B=∠1;(4)∠B与∠2互余;(5)∠A=∠2.其中正确的有(1)(2)(3)(填写所有正确的序号).
如图,在Rt△ABC中,AC⊥BC,CD⊥AB,∠1=∠2,有下列结论:(1)AC∥DE;(2)∠A=∠3;(3)∠B=∠1;(4)∠B与∠2互余;(5)∠A=∠2.其中正确的有(1)(2)(3)(填写所有正确的序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com