Question

6．如图，已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$（k＞0）交于A，B两点，且点A的横坐标为4，
（1）求k的值；
（2）利用图形直接写出不等式$\frac{1}{2}$x＞$\frac{k}{x}$的解；
（3）过原点O的另一条直线l交双曲线y=$\frac{k}{x}$（k＞0）于P，Q两点（P点在第一象限），若由点A，B，P，Q为顶点组成的四边形面积为24，求点P的坐标．

Answer 1

分析 （1）因为点A在直线y=$\frac{1}{2}$x上，故将其横坐标代入直线的解析式，求出对应的y的值，即可求得点A的坐标，再利用反比例函数图象上点的坐标特征即可求出k值；
（2）根据两函数图象的上下位置关系即可得出不等式的解集；
（3）作AM⊥x轴于点M，PN⊥x轴于点N．设P点的坐标为（a，$\frac{8}{a}$），根据正比例函数与反比例函数的对称性即可得出四边形APBQ为平行四边形，根据平行四边形的性质结合平行四边形的面积为24可得出S_△OAP=6，分点P在直线AB上方及点P在直线AB下方两种情况考虑，找出关于a的一元二次方程，解之即可得出结论．

解答 解：（1）∵直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$（k＞0）交于A，B两点，且点A的横坐标为4，
∴$\frac{1}{2}$×4=2，即：A点的坐标为（4，2），
∴k=4×2=8，
即：k的值为8．
（2）∵点A与点B关于原点O对称，
∴点B的坐标为（-4，-2），
又∵不等式$\frac{1}{2}$x＞$\frac{k}{x}$的解，是函数图象上直线位于双曲线上方的部分对应的x的取值，
∴由图象可知：不等式$\frac{1}{2}$x＞$\frac{k}{x}$的解是：-4＜x＜0和x＞4．
（3）作AM⊥x轴于点M，PN⊥x轴于点N．设P点的坐标为（a，$\frac{8}{a}$）．
∵P、Q关于O点对称，A、B关于O点对称，
∴四边形APBQ为平行四边形，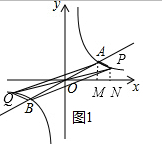
∴4S_△OAP=24，
∴S_△OAP=6．
①当点P在直线AB的下方时，如图1所示，
S_△OAP=$\frac{1}{2}$×4×2+$\frac{1}{2}$（$\frac{8}{a}$+2）（a-4）-$\frac{1}{2}$a•$\frac{8}{a}$=6，
∴a²-6a-16=0，
解得：a₁=-2，a₂=8，
∴此时点P的坐标为（8，1）；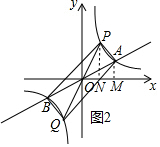
②当点P在直线AB的上方时，如图2所示，
S_△OAP=$\frac{1}{2}$a•$\frac{8}{a}$+$\frac{1}{2}$（$\frac{8}{a}$+2）（4-a）-$\frac{1}{2}$×4×2=6，
∴a²+6a-16=0，
解得：a₁=2，a₂=-8，
∴此时点P的坐标为（2，4）．
综上所述：点P的坐标为（8，1）或（2，4）．

点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及平行四边形的判定，解题的关键是：（1）求出点A的坐标；（2）利用两函数图象的上下位置关系解不等式；（3）找出关于a的一元二次方程．本题属于中档题，难度不大，解决该题型题目时，根据反比例函数图象上点的坐标特征求出反比例函数系数k是关键．