
分析 (1)根据平方差公式,可得答案;
(2)根据平方差公式,可得答案;
(3)根据平方差公式,可得答案;
(4)根据平方差公式,可得答案;
(5)根据平方差公式,可得答案.
解答 解:(1)a2-9b2=(a+3b)(a-3b);
(2)25x2y2-1=(5xy+1)(5xy-1);
(3)-$\frac{16}{9}$a2+$\frac{81}{4}$b2=($\frac{9}{2}$b+$\frac{4}{3}$a)($\frac{9}{2}$b-$\frac{4}{3}$a);
(4)(x+y)2-4=(x+y+2)(x+y-2);
(5)16(a-b)2-25(a+b)2=[4(a-b)+5(a+b)][4(a-b)-5(a+b)]
=(9a+b)(-a-9b)
=-(9a+b)(a+9b).
点评 本题考查了因式分解的意义,一提,二套,三检查,分解要彻底.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
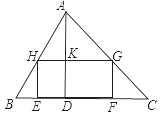 有一块三角形的余料ABC,要把它加工成矩形的零件,已知,BC=12cm,高AD=8cm,矩形EFGH的边EF在BC边上,G、H分别在AC、AB上.
有一块三角形的余料ABC,要把它加工成矩形的零件,已知,BC=12cm,高AD=8cm,矩形EFGH的边EF在BC边上,G、H分别在AC、AB上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
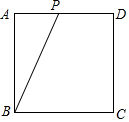 正方形ABCD的边长为2,点P是边AD上一动点(不与点A、D重合),设AP=x.
正方形ABCD的边长为2,点P是边AD上一动点(不与点A、D重合),设AP=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com