
【题目】如图:①②③中,∠A=42°,∠1=∠2,∠3=∠4,则∠O1+∠O2+∠O3=( )度.
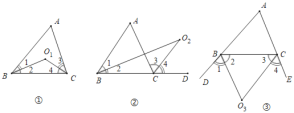
A. 84B. 111C. 225D. 201
【答案】D
【解析】
在图①②③中,分别根据三角形的内角和、外角性质及互补关系推导出∠O1、∠O2、∠O3的度数,再相加即可得答案.
解:∵①②③中,∠A=42°,∠1=∠2,∠3=∠4,
∴①中,∠2+∠4=![]() (∠1+∠2+∠3+∠4)=
(∠1+∠2+∠3+∠4)=![]() (180°﹣42°)=69°,故∠O1=180°﹣69°=111°;
(180°﹣42°)=69°,故∠O1=180°﹣69°=111°;
②中,∠O2=∠4﹣∠2=![]() [(∠3+∠4)﹣(∠1+∠2)]=
[(∠3+∠4)﹣(∠1+∠2)]=![]() ∠A=21°;
∠A=21°;
③中,∠ABC+∠ACB=180°﹣∠A=180°﹣42°=138°,则∠1+∠2+∠3+∠4=180°+180°﹣138°=222°
故∠O3=180°﹣(∠2+∠3)=180°﹣![]() ×222°=69°
×222°=69°
∴∠O1+∠O2+∠O3=111°+21°+69°=201°
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB与AD满足什么条件时,四边形MENF是正方形?说明理由.
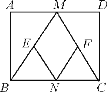
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级甲、乙两班分别选5名同学参加“学雷锋见行动”演讲比赛,其预赛成绩如图:
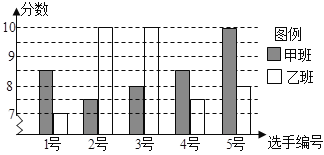
(1)根据上图求出下表中的a,b,c的值(单位:分);
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | a | 8.5 | 0.7 |
乙班 | b | 8 | c | 1.6 |
(2)学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的县级演讲比赛,求这5人预赛成绩的平均分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠AOB=90°,OC平分∠AOB,点P在射线OC上.点E在射线OA上,点F在射线OB上,且∠EPF=90°.
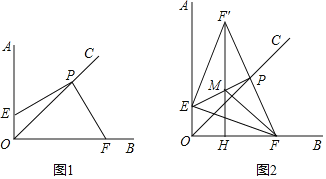
(1)如图1,求证:PE=PF;
(2)如图2,作点F关于直线EP的对称点F′,过F′点作FH⊥OF于H,连接EF′,F′H与EP交于点M.连接FM,图中与∠EFM相等的角共有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了 h;
(2)求线段DE对应的函数解析式;
(3)求轿车从甲地出发后经过多长时间追上货车.

查看答案和解析>>
科目:初中数学 来源: 题型:
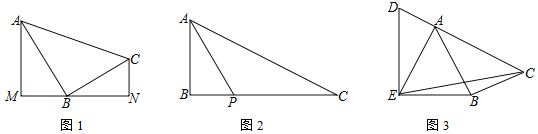
【题目】在△ABC中,∠ABC=90°.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=![]() ,求tanC的值;
,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=![]() ,
,![]() ,直接写出tan∠CEB的值.
,直接写出tan∠CEB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,AB=AC,CD是△ACB的角平分线.若在边AC上截取CE=CB,连接DE,则图中等腰三角形共有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
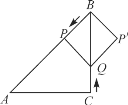
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=10cm,点P从点B出发,沿BA方向以每秒![]() cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com