
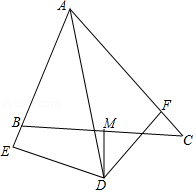
 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由角平分线的性质可知①正确;②由题意可知∠EAD=∠FAD=30°,故此可知ED=$\frac{1}{2}$,DF=$\frac{1}{2}$,从而可证明②正确;③若DM平分∠ADF,则∠EDM=90°,从而得到∠ABC为直角三角形,条件不足,不能确定,故③错误;④连接BD、DC,然后证明△EBD≌△DFC,从而得到BE=FC,从而可证明④.
解答 解:如图所示:连接BD、DC.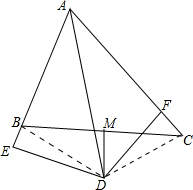
①∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴ED=DF.
∴①正确.
②∵∠EAC=60°,AD平分∠BAC,
∴∠EAD=∠FAD=30°.
∵DE⊥AB,
∴∠AED=90°.
∵∠AED=90°,∠EAD=30°,
∴ED=$\frac{1}{2}$AD.
同理:DF=$\frac{1}{2}$.
∴DE+DF=AD.
∴②正确.
③由题意可知:∠EDA=∠ADF=60°.
假设MD平分∠ADF,则∠ADM=30°.则∠EDM=90°,
又∵∠E=∠BMD=90°,
∴∠EBM=90°.
∴∠ABC=90°.
∵∠ABC是否等于90°不知道,
∴不能判定MD平分∠ADF.
故③错误.
④∵DM是BC的垂直平分线,
∴DB=DC.
在Rt△BED和Rt△CFD中
$\left\{\begin{array}{l}{DE=DF}\\{BD=DC}\end{array}\right.$,
∴Rt△BED≌Rt△CFD.
∴BE=FC.
∴AB+AC=AE-BE+AF+FC
又∵AE=AF,BE=FC,
∴AB+AC=2AE.
故④正确.
故选:C
点评 本题主要考查的是全等三角形的性质和判定、角平分线的性质、线段垂直平分线的性质,掌握本题的辅助线的作法是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
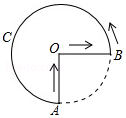 诸暨影视城里有一座圆形的土楼,如图,小王从南门点A沿AO匀速直达土楼中心古井点O处,停留拍照后,从点O沿OB也匀速走到点B,紧接着沿$\widehat{BCA}$回到南门,下面可以近似地刻画小王与土楼中心O的距离s随时间t变化的图象是( )
诸暨影视城里有一座圆形的土楼,如图,小王从南门点A沿AO匀速直达土楼中心古井点O处,停留拍照后,从点O沿OB也匀速走到点B,紧接着沿$\widehat{BCA}$回到南门,下面可以近似地刻画小王与土楼中心O的距离s随时间t变化的图象是( )| A. | 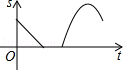 | B. | 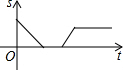 | C. | 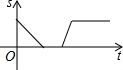 | D. | 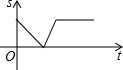 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
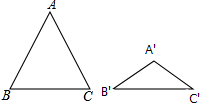 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为25:9.
如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为25:9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com