
【题目】如图,甲、乙两动点分别从正方形 ABCD 的顶点 A、C 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的 3 倍,则它们第 2018 次相遇在边( )上.
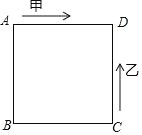
A. CDB. ADC. ABD. BC
【答案】B
【解析】
根据甲的速度是乙的速度的 3 倍,除第一次相遇路程和为两个边长外,其余每次相遇路程和都是四个边长,所以甲乙每隔四次循环一次,找到规律即可解题.
设正方形的边长为a,
∵甲的速度是乙的速度的 3 倍,
∴时间相同,甲乙的路程比是3:1,
∴第一次相遇,甲乙的路程和是2a,此时甲走了![]() a, 乙走了
a, 乙走了![]() a,在CD边相遇,
a,在CD边相遇,
第二次相遇, 甲乙的路程和是4a,此时甲走了![]() ,乙走了
,乙走了![]() ,在AD边相遇,
,在AD边相遇,
第三次相遇, 甲乙的路程和是4a,此时甲走了![]() ,乙走了
,乙走了![]() ,在AB边相遇,
,在AB边相遇,
第四次相遇, 甲乙的路程和是4a,此时甲走了![]() ,乙走了
,乙走了![]() ,在BC边相遇,
,在BC边相遇,
第五次相遇, 甲乙的路程和是4a,此时甲走了![]() ,乙走了
,乙走了![]() ,在CD边相遇,
,在CD边相遇,
......
∵2018=504![]() 4+2,
4+2,
∴它们第2018次相遇在边AD上,
故选B.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠BAC=60°,内角∠ABC、∠ACB的平分线相交于点O,则∠BOC=______;
(2)如图2,△ABC中,∠BAC=60°,AD是△ABC的边BC上的高,且∠B=∠1,求∠C的度数.
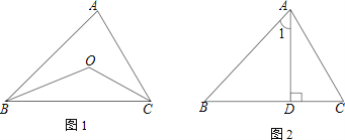
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,P为平面内的一个动点,BP=BA,0<∠PBC<180 ,DB平分∠PBC,且DB=DA.
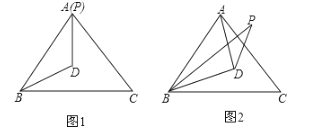
(1)当BP与BA重合时(如图1),求∠BPD的度数;
(2)当BP在∠ABC的内部时(如图2),求∠BPD的度数;
(3)当BP在∠ABC的外部时,请你直接写出∠BPD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
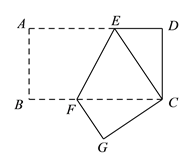
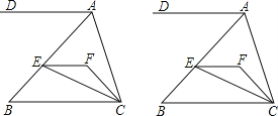
【题目】已知将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF.
(1)求证:CE=CF;
(2)若AB =8 cm,BC=16 cm,连接AF,写出求四边形AFCE面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
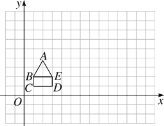
【题目】已知:如图,是由一个等边△ABE和一个矩形BCDE拼成的一个图形,其点B,C,D的坐标分别为(1,2),(1,1),(3,1).
(1)直接写出E点和A点的坐标;
(2)试以点B为位似中心,作出位似图形A1B1C1D1E1,使所作的图形与原图形的位似比为3∶1;
(3)直接写出图形A1B1C1D1E1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
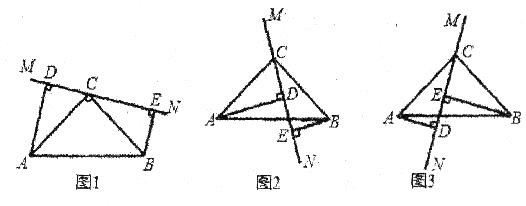
(1)①求证图1中△ADC≌△CEB;②证明DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,请说明DE=AD-BE的理由;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组条件中,能够判定△ABC≌△DEF 的是( )
A. ∠A=∠D,∠B=∠E,∠C=∠FB. AB=DE,BC=EF,∠A=∠D
C. ∠B=∠E=90°,BC=EF,AC=DFD. ∠A=∠D,AB=DF,∠B=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,![]() ,
,![]() ,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持
,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持![]() ,连接DE、DF、EF在此运动变化的过程中,下列结论:(1)
,连接DE、DF、EF在此运动变化的过程中,下列结论:(1)![]() 是等腰直角三角形;
是等腰直角三角形;![]() 四边形CDFE不可能为正方形,(3)
四边形CDFE不可能为正方形,(3)![]() 长度的最小值为4;(4)连接CF,CF恰好把四边形CDFE的面积分成1:2两部分,则
长度的最小值为4;(4)连接CF,CF恰好把四边形CDFE的面积分成1:2两部分,则![]()
![]() 或
或![]() 其中正确的结论个数是
其中正确的结论个数是

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°.
(1)求∠FEC的度数;
(2)若∠BAC=3∠B,求证:AB⊥AC;
(3)当∠DAB=______度时,∠BAC=∠AEC.(请直接填出结果,不用证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com