
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:解答题
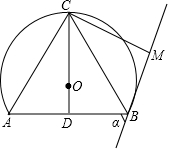 如图,若点C为优弧$\widehat{AB}$的中点,点D为AB的中点,将点D绕着点C按逆时针方向旋转60°后,得到点M,作直线BM,设BM与AB的夹角为α.
如图,若点C为优弧$\widehat{AB}$的中点,点D为AB的中点,将点D绕着点C按逆时针方向旋转60°后,得到点M,作直线BM,设BM与AB的夹角为α.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | 丙 | |
| 平均货轮载重的吨数(万吨) | 10 | 5 | 7.5 |
| 平均每吨货物可获例如(百元) | 5 | 3.6 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
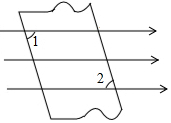 如图,一束平行光线中插入一张对边平行的纸板,若光线与纸板左上方所成的∠=65°25′,那么光线与纸板右下方所成的∠2的度数是65°25′.
如图,一束平行光线中插入一张对边平行的纸板,若光线与纸板左上方所成的∠=65°25′,那么光线与纸板右下方所成的∠2的度数是65°25′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com