分析:(1)根据已知直接求出即可;
(2)根据题目中的方法,可将1恒等变形为(2-1),套入方法可得答案.
(3)由(1)易得,22010+22009+22008+…+22+2+1=22011-1,依次分析2的次方的个位数字可得规律,运用规律可得22011的个位数字是2,进而可得答案
解答:解:(1)当x=3时,(3-1)(33+32+3+1)=34-1=81-1=80;
(2)25+24+23+22+2+1,
=1×(25+24+23+22+2+1),
=(2-1)(25+24+23+22+2+1),
=26-1,
=63;
(3)由(1)可得,22010+22009+22008+…+22+2+1=22011-1,
分析可得:2的1次方个位是2,2的2次方个位是4,2的3次方个位是8,2的4次方个位是6,
2的5次方个位是2,2的6次方个位是4,2的7次方个位是8,2的8次方个位是6,
…,四个一组,依次循环,故可得22011的个位数字是8,
则22010+22009+22008+…+22+2+1即22011-1的值的个位数是7.
点评:此题考查了尾数特征,根据已知发现规律并运用规律是解题关键,有一定难度,但认真观察,细心分析也可以求解.



 同步练习强化拓展系列答案
同步练习强化拓展系列答案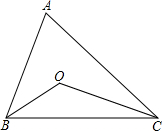 (探索题)如图△ABC中,∠ABC,∠ACB的平分线相交于点O.
(探索题)如图△ABC中,∠ABC,∠ACB的平分线相交于点O.


